
RETURN to Periodic Table
Below: Electron Shell, Bonding & Ion Formation, Magnetic Properties, Electric Properties
Chromium is the 24th element on the periodic table. It has 24 protons and 28 neutrons for a mass of 52 amu, and 24 electrons.
Electron Shell 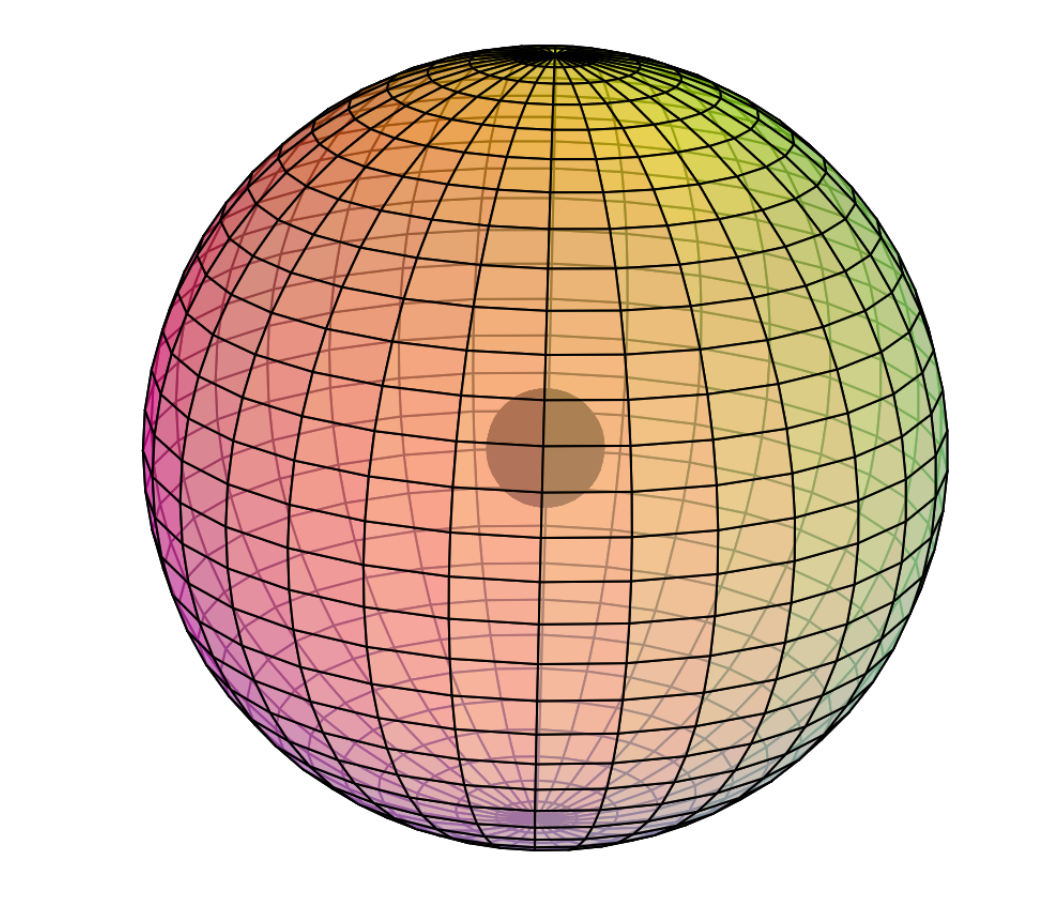
DISCLAIMER: The following reflects the sub-quantum mechanics approach to electron interactions and hybridization. Some details may therefore differ somewhat from traditional quantum chemistry:
Chromium is the fourth element to feature electrons in the d–orbital. Building upon the pd-hybridization [ref] we introduced in regard to scandium (Sc), titanium (Ti), and vanadium (V), it is proposed that chromium has a 3rd shell containing 3 di-electrons and 5 unpaired electrons in p3d5-hybridized, hexagonal bipyramidal symmetry. The three p-orbital di-electrons occupy three symmetrically distant equatorial positions to minimize repulsion. The 5 unpaired electrons occupy the remaining equatorial and axial positions. (See image below.)
This pd-hybridization does not need to involve the 3s-orbital electrons, which can remain in their preferred spherical di-electron state, within which (or upon which) the hybrid orbitals will resonate like harmonics upon a fundamental. However, one electron from the 4s-orbital must join the 3rd shell hybridization in order to achieve symmetry in eight directions, and to avoid the asymmetry of seven directions.
In such a configuration, the 4 tetrahedral 2nd shell di-electrons will align themselves with one di-electron opposite one of the single electrons in the 3rd shell, allowing all other di-electrons to orient their directions roughly between one another in order to minimize repulsion between shells.

 CLICK HERE to interact with this object
CLICK HERE to interact with this objectNOTE: The small spheres in the image above simply indicate the directions of maximum electron density. The 3rd shell hybrid orbitals themselves will assume a spherical hexagonal bipyramidal structure that divides the 3rd shell into eight roughly equal volumes, with 5-way and 3-way symmetries. Each shell segment will be filled with electron density. It will be highest at the center of the face of each orbital (as in the traditional hybrid orbital lobe shapes) and will decrease toward the nodal regions between orbitals — as wave structures usually do — where electron density will be lowest (though not zero).
NOTE ALSO: Even though it is often useful to talk about these orbitals as separate, they are all — the entire atom is — part of a single, coherent, harmonic, resonant, phase-locked, spherically-symmetrical quantum wave state, and it is all electromagnetic at the root-energy level. Orbitals and their ‘boundaries’ can be seen as nothing more than nodes and antinodes in this harmonic wave structure.
The diagram below only shows chromium’s eight 3rd shell p3d5-hybrid orbitals. (The darker color represents di-electrons, the lighter color represents unpaired electrons. The sharp edges should not be taken too literally!)
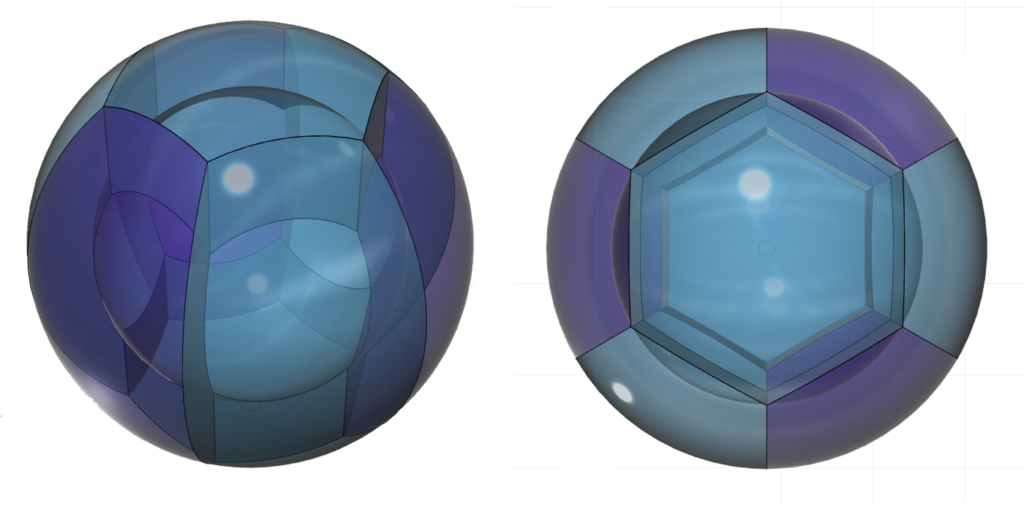
It is also proposed that the stronger repulsion and larger charge density of the three di-electrons will cause them to take up slightly more space and will therefore constrict the five unpaired degenerate electron orbitals slightly. It is expected that this would increase the magnetic signatures of these electrons. (See Magnetic Properties below.)
As in the case of scandium, titanium, and vanadium’, chromiums 3rd shell p3d5-hybrid orbitals exist within the added sheath of the 3s2-orbital di-electron, since it is not needed for hybridization. They are superimposed within it as a harmonic frequency coincides with its fundamental frequency in a resonance. It is proposed that the 3s2 di-electron gives additional stability to the electron configuration within it, even though it contains 5 unpaired electrons. The other elements in the d-block will also experience this 3s-orbital stabilization phenomenon, since they achieve at least 4-directional symmetry with only their p– and d-orbitals.
Bonding & Ion Formation 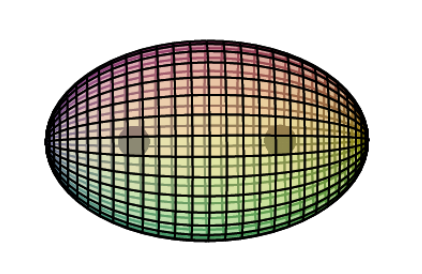
In chromium, a 4s1-orbital valence shell completes the atom. This is because one of the valence electrons drops down into the 3rd shell hybridization in order to allow it to achieve 8-directional symmetry. (This occurs in a few other cases, for example copper (Cu) and silver (Ag).)
When forming a metallic crystal, the 4s1 electron delocalizes to form the metallic bond, and when forming a 1+ ion, it is removed. In both cases, the core electron geometry remains the same. (A second ionization, however, would shift its geometry by moving the 2 remaining di-electrons into the axial positions. This assumes that one of the di-electrons will be ionized, rather than an unpaired electron, once again in order to retain 8-directional symmetry.)
Magnetic Properties 
Chromium is the only metal that is naturally antiferromagnetic at room temperature (see below), though it loses this antiferromagnetism in favor of paramagnetism at a rather low Curie Temperature of 38ºC. Let us first consider its paramagnetic strength, when compared to the paramagnetic strength of the other 3d transition metals.
Chromium has a total of six unpaired electrons, though one of these is a valence electron. In all elements prior to the d-block, unpaired electrons have occurred only in the outer (valence) shell of the atom. Those are the electrons involved in chemical reactions. Chromium is the fourth case of an atom with unpaired core electrons, and it has five of them, in addition to its single unpaired valence electron. The core electrons are protected from reacting (at least, until chromium becomes a Cr+ ion), and they are stabilized by the 3s di-electron ‘fundamental.’ We propose that it is this protection and stabilization of unpaired core electrons that allows them to interact magnetically, and that consequently determines an element’s magnetic properties.
UNPAIRED CORE ELECTRONS:
While these electrons may technically be called core electrons, for the purposes of this discussion, we recognize that in a metal, if we exclude the valence “conduction” electrons, the pd-hybrid orbital electrons do become ‘valence electrons’ in a sense. Not in the sense that they can participate in chemical reactions, but in the sense that they are now in the outermost shell of the atomic cores, which are suspended in the conduction electron matrix — the 3D electron gas — of the solid metal crystal.
PARAMAGNETISM:
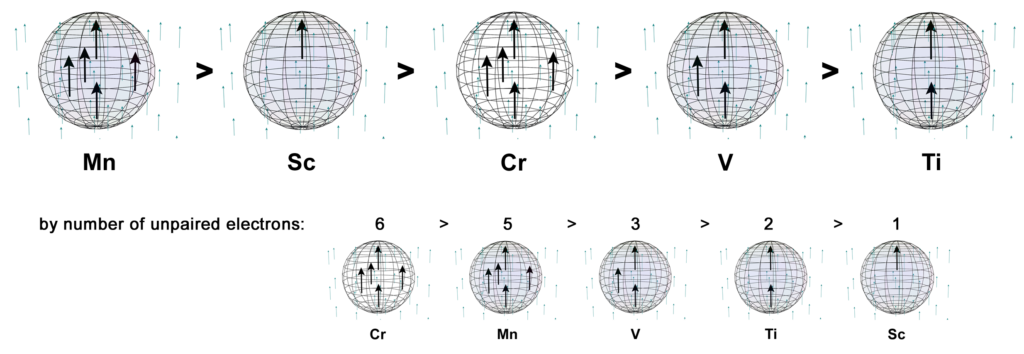
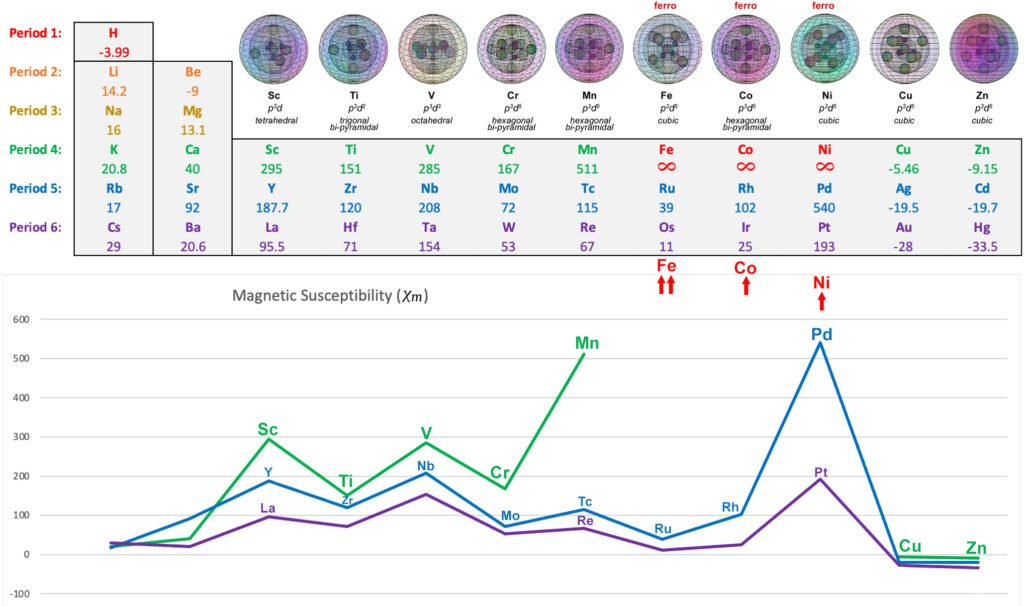
In the presence of an external magnetic field, an unpaired core electron will orient its spin to align with the magnetic field. This will cause the atom to be drawn into and toward that field — via magnetic field cancellation — giving it a positive magnetic susceptibility (χm) value. This attractive force is called paramagnetism, and its effects only last as long as the external magnetic field is present. We might therefore presume that, the stronger the paramagnetism, the more ‘unpaired electron character’ is present. Surprisingly, this does not seem to go according the number of unpaired electrons present, as the diagram below illustrates. There must therefore be other contributing factors, which we will investigate below.
When chromium is above its Curie Temperature of 38ºC, it is the third most paramagnetic metal of the 3d row — excluding the ferromagnetic iron, cobalt, and nickel — even though it has the most unpaired core electrons, with five.
As described above, it is proposed that chromium has five unpaired 3rd shell electrons arranged in a hexagonal bipyramidal electron structure. Due to orbital constriction by the 3 di-electron orbitals in the same shell, the 5 unpaired electron orbitals should be slightly compressed (and concentrated).
The images below are intended to represent the orientation of these electrons in an external (or adjacent atom’s) magnetic field (whose north pole is pointing upwards). (The purple arrows inside the atom represent the 5 unpaired electrons and the black dots represent the relative positions of the 3 di-electrons.)

 CLICK HERE to interact with this object
CLICK HERE to interact with this objectIf we exclude the 4s1 electron, chromium has five times as many unpaired core electrons as scandium (with χm = +295), yet chromium has a lower magnetic susceptibility value of only χm = +167. It is also a lower value than manganese (Mn), which also has five unpaired core electrons but with both of its 4s2 electrons. It is here proposed that this is due to the parallel spin bonding and field cancellation that occurs between its three unpaired electrons, given their proximity, degeneracy, and orbital constriction.
It is also proposed that the case of manganese (Mn) is a better approximation of the strength of this electron geometry (with χm = +511) than chromium. As in the case of vanadium, the effective magnetic electron count (EME) of both chromium and manganese’s five 3rd shell unpaired electrons will be reduced due to spin bonding and field cancellation within its equatorial and axial symmetries. Given the presence of two more equatorial electrons than in vanadium, this electron geometry becomes paramagnetic enough for manganese to have a higher χm value than scandium.
In the case of chromium, however, the presence of the electron deficient 4s1 orbital — or indeed, of the electron-deficient electron gas — may disrupt the electron coherence, even if only with respect to the external field. If so, this would weaken these electrons’ response to an external field. In this case, it results in the atom having a weaker χm value, overall, than scandium with its single unpaired electron.
If we consider scandium’s single unpaired electron to have an EME ≈ 1e– (with χm = +295), and titanium’s 2 linear spin bonding electrons to have an EME ≈ 0.51e– (with χm = +151), along with vanadium’s 3 parallel spin bonding electrons to have an EME ≈ 0.97e– (with χm = +285), then chromium’s 5 linear and parallel spin bonding electrons appear to have an EME ≈ 0.57e–. That equates to about only 0.11e– of electron signature contributed per electron. As stated, we propose that this is due to the 4s1 electron disruption.
PARAMAGNETIC STRENGTH ANALYSIS:
The following diagram shows the relative paramagnetic strengths of the transition metals, along with their proposed hybrid orbital geometries. (See paramagnetic strength trend analysis for more detail.)
ANTIFERROMAGNETISM:
As mentioned above, chromium is the only metal that is naturally antiferromagnetic at room temperature, though it loses this antiferromagnetism in favor of paramagnetism at a rather low Curie Temperature of 38ºC.
This means that there is something about chromium’s electron structure that, when it is in crystalline metallic form at room temperature, its lowest energy state occurs when the electrons on adjacent atoms in the crystal are oriented with a magnetically antiparallel arrangement.
(NOTE: In the case of electrons, magnetically antiparallel does not mean the same as opposite spins. The former is a magnetic alignment distinction; the latter is a spin component phase relationship. Electrons of opposite spin can be either magnetically parallel or antiparallel. In the case of Hund’s 2nd Rule, adjacent degenerate electrons will both align magnetically parallel and will have the same spins, in order to create the lowest energy composite state. [ref])
The precise mechanism behind chromium’s antiferromagnetic state remains a matter under investigation, though it is believed to relate to the Fermi surface geometry within the crystal (rather than the crystal periodicity itself). [Ashcroft, Ch. 33]
If we were to speculate, based upon the present sub-quantum mechanical model, it seems plausible that the driving force behind causing the electrons on adjacent atoms to align their magnetic moments antiparallel and their spins opposite might be the pairing up of the 4s1 electrons, from adjacent atoms, in the electron gas. This might then cause the degenerate, unpaired pd-hybrid electrons to orient their spins to match the spin of their valence electron, in order to resonate mutually at the lowest energy. (Their coherence might explain why and how they both determine the Fermi surface in a crystal.)
If this conjecture is correct, it would account for why none of the other 3d transition metals are naturally antiferromagnetic. Each of the other 3d metal atoms contributes 2 valence electrons to the electron gas. They therefore do not require a valence electron of opposite spin from an adjacent atom in order to find the stability of an electron coupling (or, at least, a spin-zero average), and this form of coupling is therefore not present to anti-align the core unpaired electron orbitals of adjacent atoms. (Copper is an exception, since it also donates a valence electron into its core… although it contains no unpaired core electrons, which is why it is diamagnetic.)
According to this conjecture, it would seem that chromium’s antiferromagnetism does not arise from a crystal-wide spin-bonding resonance, as it does in the case of ferromagnetism. (It would therefore not be a form of ferromagnetism. It is proposed that chromium’s unpaired electron orbitals do not experience sufficient orbital extension to be ferromagnetic, due to constriction from only 3 same-shell di-electrons.) Consequently, the crystal structure of chromium — which is body-centered cubic (BCC) — should have no meaningful bearing on the mechanism behind its antiferromagnetism (as it would have in the case of a ferromagnetic crystal).
It is therefore proposed that the antiferromagnetism of chromium arises from an electron coupling resonance within the (valence) electron gas that binds the crystal. (This region is where the above-mentioned Fermi surface, as well as the valence and conduction bands are located.) Thus, even though the unpaired core electrons are not significantly extended, it is proposed that they do not need to be in order to resonate in degeneracy — to couple — with their own valence electron. (Perhaps we might even think of it as a kind of ‘local paramagnetism.’)
Since the coupling valence electron from each adjacent nearest-neighbor atom will have opposite spin, the (magnetic) core electrons of these adjacent atoms will therefore have opposite spins.
When the temperature increases enough to reach the Curie temperature, however, there is enough thermalization present to disrupt this weak electron gas coupling resonance, to the point where an external magnetic field will overwhelm it in favor of a crystal-wide paramagnetic alignment with the now-dominant external field. If this field is removed, the crystal will remain paramagnetic — with random magnetic alignments of the core electrons — until it cools below its Curie Temperature, at which time the electron gas coupling resonance can gain enough ‘traction’ over thermalization to re-enable antiferromagnetism.
Electrical Properties 
It is interesting to note that the three best electrical conductors — silver (Ag), copper (Cu), and gold (Au) — all share a feature with chromium: a single valence s-orbital electron. However, chromium is a much weaker electrical conductor.
We might speculate that such an ‘activated,’ electron-deficient valence conduction band may actually promote the passage of electrical potential. It may simply offer less resistance to it (by having more unoccupied energy states in the band structure that are available to transmit electrons).
What separates the three precious-metal good conductors from chromium is the nature of their core electron resonances. In the three precious metal elements, the inner orbitals are all completely filled with di-electrons, which are diamagnetic. We might speculate then that, upon this ‘non-interfering’ foundation, the single-valence-electron conduction band may support the transmission of electrical potential through the metallic crystal quite effectively. In the case of chromium, however, there are five unpaired electrons on the surface of every atomic core in the crystal. Their magnetic field and spin interactions might interfere with the electrons in the conduction band in such a way that diminishes conductivity, due to resistance. It is further conceivable that, given the ratio of electrons involved, it may decrease chromium’s conductivity to merely one tenth of the conductivity of copper and silver.
Credence for this conjecture might come from the fact that, even though chromium has a much lower electrical conductivity than copper, it nevertheless has a much higher conductivity than its immediate neighbors in the 3d-block — vanadium (V) and manganese (Mn) — which each have full valence 4s2-orbitals. (Though this fact is not conclusive on its own.)
RETURN to the Periodic Table
OTHER PARAMAGNETIC 3d METALS: Scandium, Titanium, Vanadium, Chromium (also antiferromagnetic), Manganese
FERROMAGNETIC 3d METALS: Iron, Cobalt, Nickel
DIAMAGNETIC 3d METALS: Copper, Zinc
