Breakthroughs

---

1. The Substructure of the electron

From its discovery by J.J. Thomson in 1897, the electron was believed to be a point particle with no substructure. Its charge could be measured, experimentally, to be -1.6 x 10^-19 Coulombs, but the how and why of that charge remained a mystery. The electron was also observed to have a property called spin, as well as an anomalous magnetic moment (called g-2). Like its charge, these properties could also not be calculated from theory alone.

In addition to being considered point particles with no substructure, electrons are also believed to be much smaller than a proton, but in the hydrogen atom, for example, the electron is the size of the atom. In the solid state, electrons can actually be many times larger than an atom (see Misconception Series: The Size of the Electron).

The electron’s properties must be a consequence of its substructure. Detail of this substructure was proposed by Dr. John G. Williamson (inventor of the first semiconductor device to be dubbed “nano” — the quantum point contact) and Dr. Martin B. van der Mark in their 1997 paper (see it here), as well as being further developed and reinforced in several subsequent papers (for example this one). Based on their theory, both the charge of the electron and its anomalous magnetic moment can be calculated, a priori.

For more on this charge calculation, see Calculating The Electron Charge.

The nature of the electron

An electron-positron pair is formed when two photons of the appropriate energy are condensed, forming two particles. One of the resulting double-loops with its electric field (the green spines) pointing outwards will have a positive charge — the positron, and the other, with its electric field pointing inwards, will have a negative charge — the electron. Similarly, when an electron and a positron interact, they unlock each other’s angular momenta, releasing the once-confined photons as radiation in a matter-antimatter annihilation.

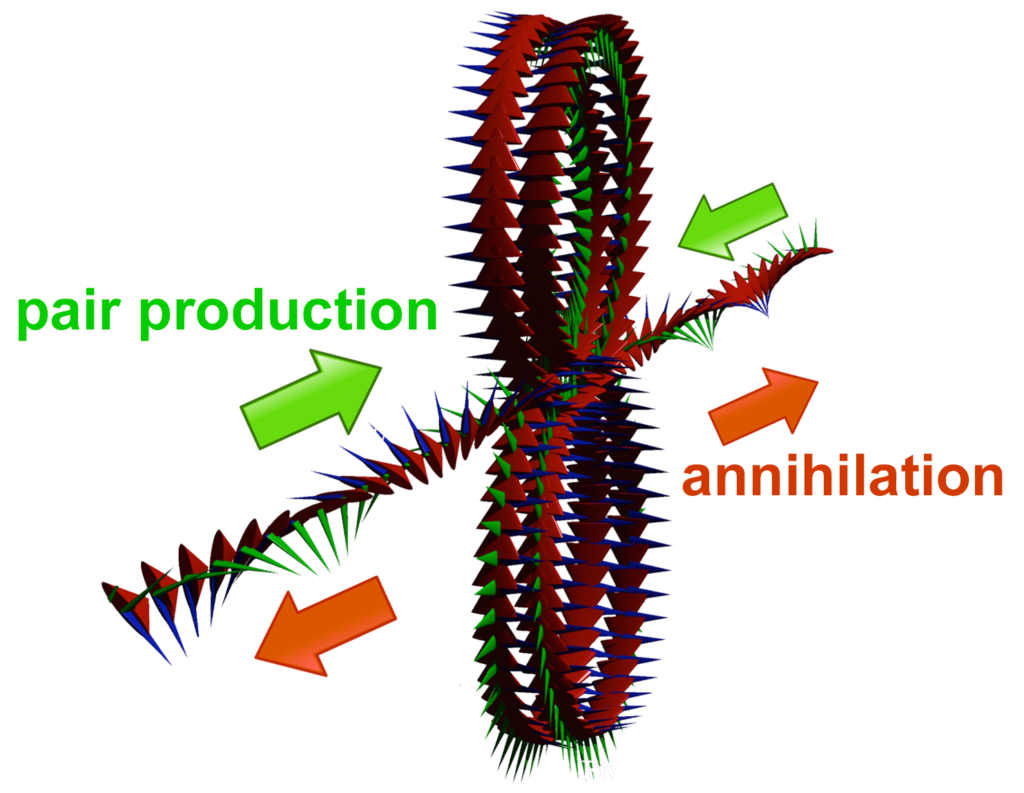
Each particle contains a confined photon making two complete revolutions for every one wavelength, which allows the photon’s fields to lock in on themselves. This results in a phase-locked, stationary wave of toroidal topology that defines the particle. As a result of the rotation, the photon’s electric field is always outwardly directed, resulting in its charge.

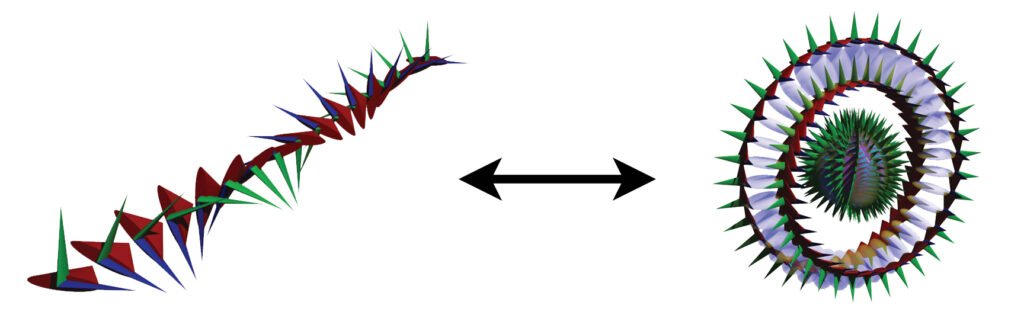
The snapshot of the electron (above, right) can be misleading because it is really many images combined. In normal space, each lens-shaped disk represents a slice through the same spherical distribution. The toroidal (donut) shape represents the phase-locked path of the rotating photon in momentum space (spatial frequency space ). In order to conserve the circularly-polarized photon’s angular momentum, the toroid will also tumble in space like a head-over-heels spinning ring (). The sphere in the center represents the result of this — a projection onto normal 3-dimensional space of the electron’s charge distribution, which is perfectly spherical in normal “space-space” ().

An isolated electron is thus a self-confined knot of concentrated energy traveling around itself at the speed of light.

CLICK HERE to see one of John Williamson’s lectures on the subject.

This revolutionary work explains (and unifies) the electron’s shared particle and wave nature, and it similarly — and notably — bridges the gap between the quantum and classical realms. While an electron is a particle, its underlying nature is electromagnetic, containing a photon, which itself has both wave and particle properties. It is held together by a powerful coherence, far stronger than the strong nuclear force, here dubbed the “super strong force.” Furthermore, it is these topologies — hbar of photon angular momentum and ½hbar of internal particle angular momentum — which lie at the very heart of quantization itself.

Electrons are harmonic stationary waves that have electric charge, magnetic field, and angular momentum, and they are affected by the charge, field, and spin of other particles in their vicinity. As a result, when multiple electrons interact in the same atom or molecule, they produce orbital regions that are symmetrical, phase-locked, resonant, coherent, spherically-harmonic, stationary electron waves. These stationary waves represent a maximum symmetry state of the system, incorporating regions of positive and negative wave interference. Note that within this new theory of quantum electromagnetism, these coherent states need not be simply the lowest energy states. Quasi-stable coherent states of higher energy may include, for example, a spin coherence.

The entire atomic system forms a single, coherent, harmonic quantum state. Each electron within this state can no longer be seen as an independent particle but as an essential component of the harmonic electron stationary wave. Any addition or subtraction of energy or electrons will cause the entire system to snap into its next most stable harmonic state.

For more information, see Understanding Electrons.

For a selection of video lectures by Dr. John G. Williamson on this and other topics, click HERE.

For a brief video overview of Sub-Quantum Mechanics and some applications of this understanding of electron substructure to quantum spin, electron bonding, and matter-antimatter annihilation, click HERE.

Related glossary entries:
– MART, the Mathematics Of Absolute Relativity Theory
– Root-energy
– Sub-quantum mechanics
– Williamson equation

BACK TO TOP

---

2. Robinson Model of Nuclear Binding

For many years, the forces operating at the nuclear level have been called simply the strong nuclear force and the weak nuclear force. Their precise origins and mechanisms of operation, however, have remained unclear, as have the nature and substructures of the proton and neutron that give them their distinctive properties. (While much has been published on the subject of quarks, they have never been isolated. As such, the concept may more correctly apply to fractional structural components within the nucleon resonance that do not occur except as part of such a resonance.)

It has long been known that the neutrons in the nucleus serve the important function of separating the mutually-repelling protons from one another, but how exactly do neutral neutrons bind to positive protons in the first place, let alone overcome mutual proton repulsion?

An important advance in our understanding of nuclear structure and the forces responsible for holding it all together has been developed by Dr. Vivian Robinson (inventor of the Robinson Backscattered Electron Detector). The Robinson Model Of Nuclear Binding is presented in chapter 5 of his book The Common Sense Universe. Some of its basic elements are described below, but for the full and compelling detail, as well as the degree to which it accords with observation and experiment, we refer you to this remarkable book.

CLICK HERE to see one of Viv Robinson’s lectures on the subject.

The nature of nucleon binding

Building upon his own conception of the electron as a particle comprised of a photon completing two revolutions per wavelength, Robinson investigated the proton and neutron in terms of having a similar photonic substructure. According to his model:

THE PROTON:
The proton is made of a circularly-polarized photon of the appropriate energy completing two revolutions per wavelength. Unlike the electron, however, the proton carries a much higher energy and therefore contains a particle resonance with superimposed harmonics. These are designated as 1/3^rd and 1/9^th harmonics.

In the diagrams below, pink represents positive charge and blue represents negative charge.

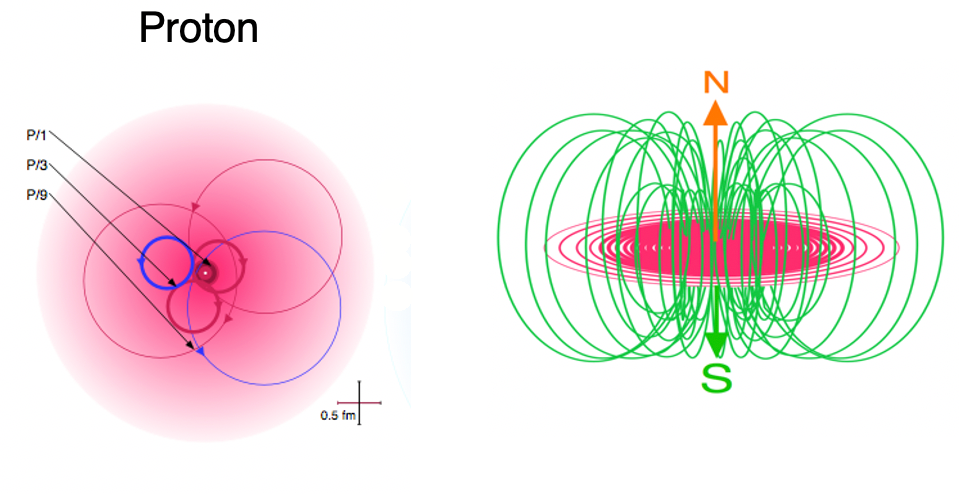
The orientation of the circularly-polarized photon’s electric field, as it makes its double loop rotation, is such that the positive field is outwardly directed for the majority of these harmonic oscillations, and in particular, the outermost one. This results in a net positive charge for the particle. This charge field emanates from the equatorial plane of the particle, in which the photon is rotating, from where the charge spreads out into the third dimension. The magnetic field lies in the axial direction, giving the particle a roughly spherical profile overall.

THE NEUTRON:
The neutron is made of a plane-polarized photon of the appropriate energy completing two revolutions per wavelength. Like the proton, it carries a much higher energy than the electron, and therefore contains a particle resonance with superimposed harmonics. These are designated as 1/3^rd, 1/9^th, and 1/27^th harmonics.

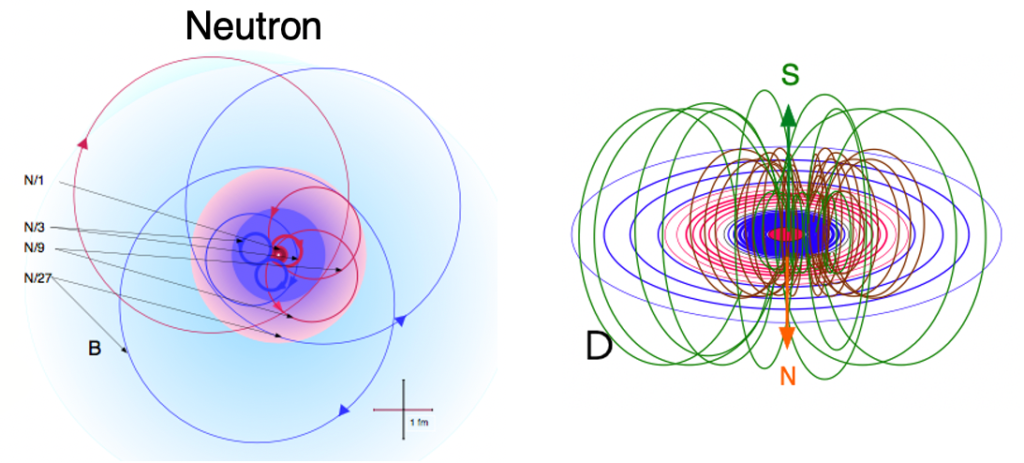
The orientation of the plane-polarized photon’s electric field, as it makes its double loop rotation, is such that the positive and negative fields are each outwardly directed in half of these harmonic oscillations, yielding a particle with no net charge overall. Like the proton, its magnetic field lies in the axial direction, giving the particle a roughly spherical profile overall.

It is the plane-polarization of the photon constituting the neutron that renders it an unstable particle when it is not bonded within a nucleus. Attraction to a proton keeps the neutron resonance stable, but an isolated neutron will decay (with a half-life of about 15 minutes) into a proton, an electron, and an anti-electron neutrino (in order to conserve angular momentum).

Significantly, the neutron’s outermost (1/27^th) harmonic carries a negative charge, and this allows protons and neutrons to attract each other and bond electrostatically in a planar, equatorial orientation, forming flat nucleon layers.

The following diagrams clarify how the opposite charge overlap effects electrostatic bonding between protons and neutrons. In both upper and lower diagrams, the height of the graph represents the intensity or density of the charge, with pink representing positive charge and blue representing negative charge.

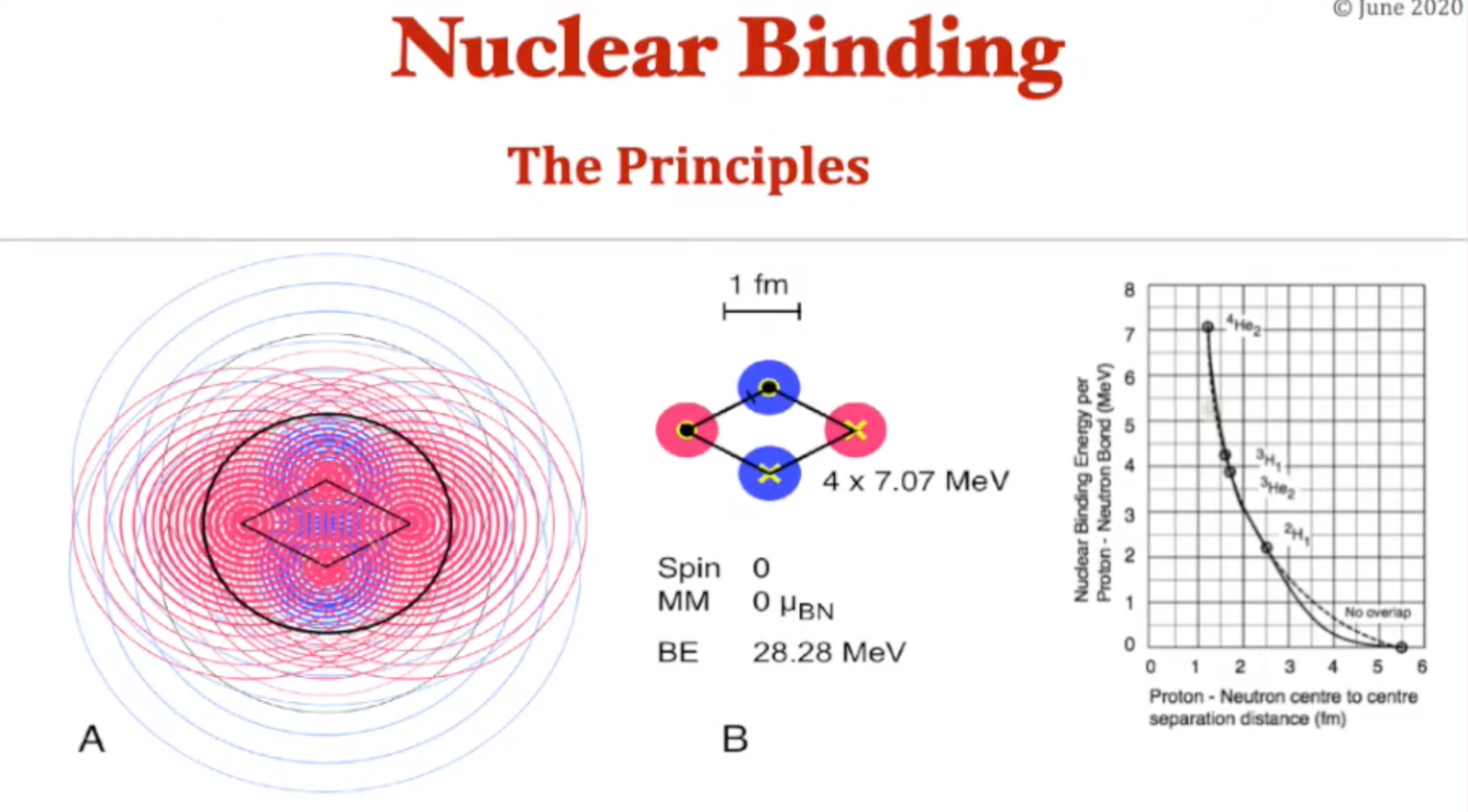
THE ALPHA PARTICLE:
The alpha particle (which is a He²⁺ ion) is an important example of such a planar nucleon layer. Two protons are held near each other by the attraction of the negatively charged exterior resonances of the two neutrons in the center. The competing forces of attraction and repulsion cause the alpha particle’s diamond shape. The protons are attracted inwards towards the neutrons, but are also repelled from one another. The neutrons are attracted towards the center by their pull towards both protons, but their mutual (though much weaker) repulsion also keeps them apart, though not as far apart as the more strongly repelling protons.

The O and the X in the diagram above denote the orientation of the nucleon’s spin (shown with arrows in the diagram below). Since the alpha particle contains one proton and one neutron of each spin, it has a net zero nuclear spin. (It can therefore be thought of as a di-boson.)

Nucleus formation

While the charge of the nucleons emerges at their equatorial circumference, their magnetic fields loop around toroidally, with their greatest density in the axial directions.

As nucleons add into a second layer, they will orient themselves in such a way that brings their north magnetic pole facing the south magnetic pole of the nucleon in the layer beneath it, or vice versa.

Like nucleons are able to bond magnetically if they are aligned axially with their magnetic moments aligned parallel. Their like-charge repulsion does not interfere with this magnetic bonding because it lies in the equatorial direction.

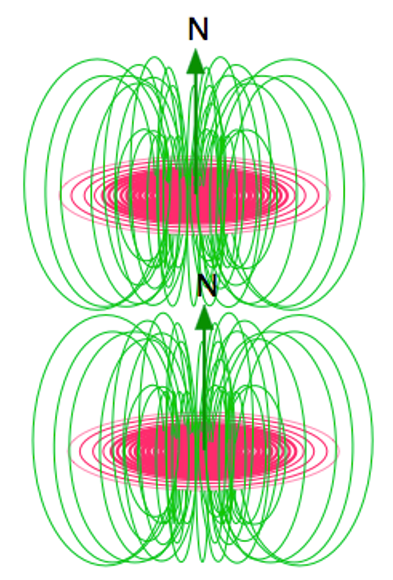
An atomic nucleus is therefore comprised of:

1. planar sheets of nucleons bonded electrostatically in a side-to-side fashion
2. layers of planar nucleon sheets bonded to each other magnetically.

The largest layers will lie in the center of the stack, with the smallest at the edges, giving a nucleus a roughly spherical profile.

By way of example, the following diagram represents two possible nucleon layer configurations for the carbon-12 (¹²C) isotope. One involves a stack of 3 alpha particles (left) and the other, a stack of 2 lithium-6 (⁶Li) nuclei (right).

The configuration on the right is more likely since there is research indicating that the carbon nucleus has been observed to have a triangular shape, with its positive charge concentrated around its circumference.

While the layers are shown above as one beside the other, in reality, they stack like flat layers, as in the diagram below.

The following diagram represents the nuclear layers of the most abundant isotope of lead (Pb).

We can now see why it is that radioactive nuclei eject nucleons in units of alpha particles. Aside from their great stability (as di-bosons), most nuclear layers are, in fact, comprised of alpha particle units.

This brief excerpt from his work clarifies that both the strong and weak nuclear forces are electromagnetic in nature.

 For a selection of video lectures by Dr. Vivian Robinson on this and other topics, click HERE.

Related glossary entries:
– electron
– neutrino
– neutron
– proton
– radioactivity

BACK TO TOP

---

3. The Robinson Theory of Sub-Quantum Gravity

(Summarized and abbreviated from Dr. Vivian Robinson’s book “The Common Sense Universe.” For full details, explanations, and derivations, refer to chapters 8-11.)

 A VIDEO on this material can be found HERE. For the presentation after which that Q&A follows, click here: ‘Visualizing Sub-Quantum Gravity‘ by Dr. Vivian Robinson.
To see the journal article (J. Phys. Commun., 2021), click HERE.

---

PART 1: The Equation of Sub-Quantum Gravity
PART 2: The Mechanism Of Gravity
PART 3: Consequences

Introduction

Gravity is a very weak force exerted by one mass upon another. In fact, it is about 10³⁸ times weaker than electromagnetism. In the late 17^th century, Isaac Newton codified the inverse-square Law of Universal Gravitation, F_N=GMm/r². This equation describes that the force (F) of attraction exerted by one mass (M) upon another mass (m) gets weaker with (the square of the) distance (r). (The gravitational constant G=6.674×10⁻¹¹ m³kg⁻¹s⁻².) From this equation we derive that the acceleration due to gravity is g_N=GM/r².

In the early 20^th century, Einstein’s General Theory of Relativity extended it into the relativistic realm. This was necessary because Newton’s equations are based on the limits of perception at the time — that the speed of light appeared to be infinite and the mass of the photon to be zero. Instead, photons are ‘particles’ of variable mass and constant (finite) velocity. Newton’s gravity had no reason to act. It was just accepted as an unknown “attraction at a distance.” Einstein developed the idea that gravity was caused by mass distorting spacetime. That gave a physical reason for gravity to exist.

Despite the utility of the gravitational field equations from Einstein’s General Theory of Relativity, a new (or updated) theory of gravity is still needed because the mechanism by which gravity occurs has not yet been explained. It is also not yet known whether it is mediated electromagnetically or via a unique gravitational particle (or boson)? Einstein’s GTR only explains that mass distorts the fabric of spacetime, which gives rise to gravity. It does not explain the nature of this fabric nor the mechanism by which the distortion occurs. While the GTR adds clarity and depth to Newton’s Law of Universal Gravitation, it is noteworthy that it only reveals the difference between a relativistic and a classical calculation of gravity. In addition, a particular detail of Einstein’s work has been misinterpreted by many over the years because a concept is applied outside of its intended constraint, and this has led to an erroneous understanding (as will be explained below).

A new theory of sub-quantum gravity has been proposed in which the quantum properties of matter, arising from their substructure, generate the distortions in spacetime that result in gravity. The specific mechanism by which mass distorts spacetime has also been proposed. This approach results in a single, simple differential equation — an equation of sub-quantum gravity — that derives:

• Newton’s inverse square law as a first approximation,
• Einstein’s field equations as a second approximation,
• and the bright torus-shaped accretion disc observed around massive objects and galaxy centers as an exact solution.

PART 1: The Equation of Sub-Quantum Gravity

EINSTEIN’S APPROXIMATION:
Einstein made an approximation in his general relativity calculations for the purpose of simplifying the mathematics, but it was only true within a certain constraint that he stated. When taken as an exact solution outside of the constraint imposed by Einstein, however, it leads to a conclusion that is not supported by observation (or Einstein’s intent).

In his 1916 paper on general relativity, Einstein’s expansion of g_𝜇𝜈 derives that the terms g₁₁ =

THE STRONG FIELD SOLUTION:
Schwarzschild and others used the above approximation to determine an exact solution of Einstein’s equation, the so-called “strong field” solution, even in cases when r is not much larger than 𝛼. This implies that gravity becomes slightly stronger than inverse square in the presence of mass, and, when r = 𝛼, that gravitational infinities are mathematically possible. In the physical universe, such infinities would result in singularities, or black holes. 

Significantly, there is no known process in nature that can generate infinite energy or that exhibits infinite strength. A mathematical infinity does not necessarily equate to a physical infinity. If anything, it points to an imprecise model specifically because we see no evidence of forces or energies of infinite magnitude in the observable universe, not to mention that they would require infinite energy. (For an exact solution to Einstein’s Gravitational Field Equations, see chapter 8 of Robinson’s book “The Common Sense Universe.”)

The Schwarzschild strong field solution also contradicts the observation that the perihelion of planetary orbits (like Mercury) and stellar orbits (like S2) precess.

ORBITAL PRECESSION:
In his Proposition 45, Newton clarified that, if the strength of gravity were exactly equal to inverse-square, the perihelion of a planet or star’s elliptical orbit would occur at the same relative position in space on each successive orbit. If gravity were stronger than inverse-square, the perihelion would regress (in the opposite direction to its travel), and if gravity were weaker than inverse-square, the position of the perihelion would precess (in the direction of its travel). Precession is what is observed.

Robinson explains that the reason for precession is that a slightly weaker gravity will hold the planet in a slightly more distant orbit. It will therefore take slightly longer to return to its perihelion position, which would therefore be a little further forward along its direction of travel.

Since Mercury’s orbit precesses, this proves that gravity becomes weaker than inverse square, not stronger, in the presence of mass. Schwarzschild’s strong field solution is therefore not compatible with either Einsteinian or Newtonian gravity.

REDSHIFT (z):
Redshift is not only caused by the Doppler Effect, but also results from a photon losing energy.

One such case occurs when a photon moves away from the gravitational field of the star that emitted it. Photons have inertial mass (m_p=h𝜈/c²), and they are therefore subject to the effects of gravity. Such interactions will reduce their energy. A reduction in energy means a reduction in frequency (E=h𝜈), and since the speed of light is constant for every observer, this results in an increase in wavelength. When photons pass a massive object, they are blue-shifted as they approach and redshifted as they move away, resulting in a net-zero overall redshift, even as they experience gravitational lensing. As we will see below, a similar refraction occurs in photon interactions with mass at the nanoscopic level, whether those photons are traveling linearly or rotating within subatomic particles.

Another case of redshift occurs when a photon travels through a medium to which it loses energy — one with an increased ‘viscosity’ or refractive index. According to the Robinson Model, space is such a medium, not simply by virtue of the mass and radiation distributed throughout it and extending their field effects, but also because it is pervaded by a density of cosmic neutrinos. These provide a continuous ‘substrate’ or matrix of rotating photon field distortions (i.e. electromagnetic waves) to every point in space, and through which every photon must proagate. (Refer to chapter 11 of The Common Sense Universe for details.) As such, the Doppler Effect need not be invoked in order to account for the redshift of cosmic photons.

Photons are thus redshifted by mass, and significantly, gravity can then be understood in terms of photon redshift. (see also Robinson, J. Phys. Commun. 5 (2021)). We will examine the specific mechanism of this gravitational effect below.

The redshift (z) of wavelength is given by z = (𝜆_r-𝜆₀)/𝜆₀.
This can be expressed as z = e^𝛼/2r-1.
When r ≫ 𝛼, this becomes z = 𝛼/2r.
(Refer to chapter 8 of The Common Sense Universe for derivation details.)

THE REDSHIFT METRIC:
Mass distorts (wave)lengths, increasing them by the redshift (z) of photons, and mass distorts time, decreasing frequencies by the redshift of photons. This correction converts Newtonian gravity as follows:

Applying this redshift metric to Newtonian gravity allows us to calculate Einsteinian general relativistic effects, including gravitational lensing and orbital precession, that match observation. By way of example, Mercury’s orbit is observed to precess by an amount of 42.98 arc seconds per century. When calculated using the redshift metric, it yields 42.99 arc seconds per century.

COMPARING THE METRICS:
The equations representing the Newton (N), Einstein (E), Schwarzschild (S), and Redshift (z) metrics are compared graphically below. These equations allow us to directly calculate the strength of the gravitational field at any distance, r, from a center of mass, M. (Note: Einstein’s gravitational field equations do not do this. They measure the distortion away from Euclidian space, which must then be added to Newton’s inverse square law to calculate the strength of the gravitational field.)

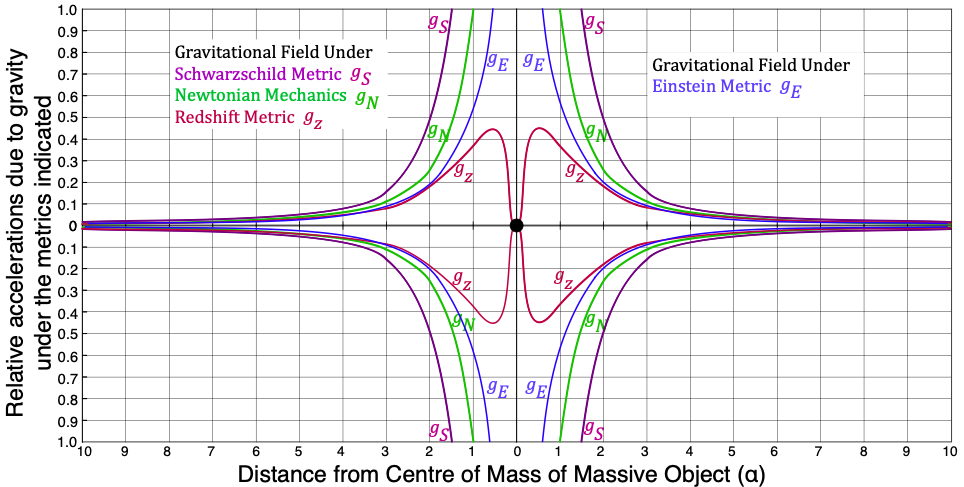
Notable features of this comparison include:

• The redshift metric applies for all values of r/𝛼. The Schwarzschild metric applies only when r ≫ 𝛼, and the Einsteinian metric when r > 3𝛼.
• When r = 10𝛼, the three metrics shown agree to within 10% of each other.
• At about r = 5𝛼, the three metrics begin to disagree significantly.
• Newtonian gravity tends to infinity as r approaches 0.
• Schwarzschild gravity tends to infinity as r approaches 𝛼.
• When r ≫ 𝛼, it is not possible to distinguish between the Einsteinian and Redshift metrics.
• Sub-quantum gravity reaches a maximum when r = 0.5𝛼.
• Sub-quantum gravity becomes weaker when r < 0.5𝛼 because spacetime distortion dominates the inverse-square law.

In considering this last point, recall Newton’s shell theorem. A body within a spherical shell of uniform density (and any thickness) will not experience any gravitational attraction from the shell around it. This means that, at the center of a massive star, while pressure is very high, gravity is weakened due to the degree to which mass is distorting spacetime.

What is more, the redshift metric thus explains why we should expect to see a torus-shaped accretion disc (or radiation distribution) around very massive objects at a distance of approximately r = 0.5𝛼 (as seen in the Event Horizon Telescope Collaboration image in 2019 ). This is where gravity is strongest. It also implies that the center should experience an outward gravitational attraction. (We will return to this point below.)

PART 2: The Mechanism Of Gravity

Gravity — the distortion of spacetime by mass — occurs as a result of the redshift of photons. (Recall that massive particles are comprised of rotating photons — see above.)

The nature of this spacetime distortion — the mechanism by which gravity occurs — is that the presence of mass induces changes in the electric permittivity (ε₀) of the free space surrounding it. (It similarly induces changes in the magnetic permeability (μ₀) of space. These two properties are related to the speed of light (c) in a fixed ratio, as determined by Maxwell, and given by the equation c² = 1/ε₀μ₀.) For convenience, μ₀ is set at a fixed value. Only changes in ε₀ are considered.

The nature of spacetime is such that the presence of alternating electric or magnetic fields affects the ε₀, an effect that diminishes with distance. As we will see below, that alternating field comes from the high frequency oscillations of the rotating photons that are the protons and neutrons in the massive object. This, in turn, affects the way that photons respond when entering that region of distorted space.

The following will clarify:

• That mass changes the electric permittivity of space (ε₀),
• How mass generates changes in ε₀,
• What happens to photons when mass distorts spacetime through changes in ε₀,
• Why mass responds to changes in ε₀ in the same way that photons do.

VARIATIONS IN ε₀ WITH DISTANCE:
In an attempt to explain the bending of light by the Sun (in 1911), Einstein suggested it could be bent by a change in the refractive index of space.

It can be derived that the refractive index (n) of a medium (_m) is given by the equation n² = ε_mμ_m/ε₀μ₀. Since Maxwell, it has been known that the refractive index of a medium is governed by its electric permittivity (ε) when the value of the magnetic permeability (μ) is fixed. When we consider it fixed, this simplifies the equation for refractive index to be n² = ε_m/ε₀.

The speed of light in a medium (c_m) will therefore be given by c_m² = c²ε₀/ε_m, which shows that the electric permittivity of space affects the speed of light through that space. An increase in refractive index resulting from an increase in ε will slow light and cause it to be refracted towards the increased ε. (Note that the speed of light will not be affected for the observer in that space.) When there is a change in the refractive index, photons are deflected.

It can further be derived that ε_m/ε₀ = (1+z)² = e^𝛼/r, in which we find the same redshift terms as we encountered above. This shows that the mass-induced changes in the electric permittivity of space are directly proportional to the gravitational attraction under the redshift metric. Photon redshift and refraction due to changes in ε₀ are the same as those due to gravity.

The value of ε_m decreases with distance from a center of mass until it reaches ε₀, the permittivity of matter-free space. (This differential is depicted by the grey gradient in the diagram below.) As a photon moves away from a center of mass, its velocity will therefore increase from c_m back to c. This will stretch its wavelength, resulting in a redshift, as has been observed. If the photon is traveling radially away from the mass (like photon B in the diagram below), its path will not be deflected. If it travels obliquely past a mass (like photon A in the diagram below), it will also experience a refraction. That refraction is the deflection caused by the refractive index gradient.

HOW MASS CHANGES ε₀:
The rotating photon model of matter, referenced above, describes the origin of and physical reasons for properties such as the special relativity corrections, why E=mc², the de Broglie wavelength, chirality, parity, the distribution of charge and magnetic field, and more. (See Robinson, chapters 2 & 3.)

The frequency of the rotating photons that comprise the nucleons is given by 𝜈 = m_Nc²/h, where m_N represents the mass of the nucleons. Accordingly, we can calculate:

• PROTON:
  • Fundamental frequency: 2.269 x 10²³ Hz.
  • Harmonic frequencies: 7.56 & 2.52 x 10²² Hz.
• NEUTRON:
  • Fundamental frequency: 2.269 x 10²³ Hz.
  • Harmonic frequencies: 7.56 & 2.52 & 0.84 x 10²² Hz
• ELECTRON:
  • Fundamental frequency: 1.24 x 10²⁰ Hz.

These photon oscillations generate commensurate oscillations in the local electric and magnetic fields. Since electric field varies as the inverse square of distance and magnetic field as the inverse cube of distance, magnetic field strength drops off much more quickly than electric field strength. This is the reason that, from a practical standpoint, we need only consider the electric permittivity (ε) effects.

The high frequency electric fields of the nucleons oscillate at about 10²⁴ Hz. This changes the electric permittivity of space, and through that, its refractive index. The gradient of the refractive index alters the paths of photons.

By incorporating the work of Feinmann on refractive index, Robinson derives that the redshift (z) at a distance (r) from a large number of nucleons (N) is given by the equation z = 2.1 x 10^-63N/r. This illustrates why gravity is so weak, and why it requires such a large number of nucleons to change ε₀ to ε_m in order to have a detectable effect. (See Robinson, chapter 9 for more detail.)

THE EFFECT ON MATTER:
Since all particles are made of rotating photons, they will all respond to changes in the electric permittivity (ε) of space in the same manner, irrespective of their orientation.

When passing near a massive object, as in the diagram above, linear photons pass quickly from one value of electric permittivity to the next and are therefore deflected only slightly. Rotating photons (that are particles) do not travel at the speed of light but tend to remain in one location. Their rotating photons are repeatedly subject to the same slight deflection, and since their photons rotate with such a high frequency, the many small deflections add up to a more significant gravitational deflection.

The mutual attraction between two masses, M and m, is caused because each changes the electric permittivity of space, to which the rotating photons in the other respond by being deflected towards it.

Gravitational waves are variations in the electric permittivity of space that propagate as a result of the movement of the massive body causing it. These waves travel at the speed of light, which is a property determined by the electric permittivity and magnetic permeability of space.

SUMMARY:
Gravity is caused by a change in the refractive index (n) of space, which is caused by the radial differential of the electric permittivity (ε) of space. In turn, this is induced by the high frequency electric field oscillations resulting from the rotating photon structure of nucleons. The high frequency nucleon oscillations add to produce a variation in electric permittivity that produces the same deflection for photons of all frequencies.

Linear photons, light, pass quickly through the changing refractive index and are hardly deflected. Rotating photons, i.e., particles, experience the same deflection. Because they stay in the one place, the deflections on each rotation add up. If the mass is unsupported, it experiences an acceleration due to this gravity. If supported, it exerts a slight force on the supporting medium, changing its mass to a weight.

This approach results in a single, simple equation — an equation of sub-quantum gravity — that derives Newton’s inverse square law as a first approximation, Einstein’s field equations as a second approximation, and the bright torus-shaped accretion disc observed (at r = 0.5𝛼) around massive objects and galaxy centers as an exact solution.

Gravity is therefore an electromagnetic effect. It is only attractive (as opposed to being attractive and repulsive like electromagnetism) because it is a refraction always towards the increased electric permittivity (ε_m) of space associated with mass.

A key result of this model is that gravity becomes weaker than inverse square when mass becomes larger. This is not only predicted by this model but observed in the “anomalous” precession of the orbits of Mercury (around the Sun) and S2 (around Sagittarius A).

PART 3: Consequences

Gravity Is Electromagnetic:
Gravity is an electromagnetic effect. It is caused by the movement and configuration of electromagnetic radiation (photons), and it affects the electric property of spacetime in such a way that affects (via redshift) other electromagnetic radiation.

Gravity is only attractive (as opposed to being attractive and repulsive like electromagnetism) because it is a refraction always towards the increased electric permittivity (ε_m) of space associated with mass.

Neutron Stars & Hydrogen Recycling:
Under the standard model of matter, protons and neutrons are quarks held together by gluons. They can only withstand a certain force before the gluons can no longer hold them. When that occurs, the neutrons collapse to form “black holes.” This is believed to occur in neutron stars with a mass of about 10 solar masses. Under the rotating photon model, a neutron does not have constituent structures, and there is no denser coherent photon resonance to which it can collapse and remain a coherent (massive) photon resonance. They can therefore be compressed by any gravitational force, and they will remain neutrons.

According to the redshift metric, gravity decreases from its maximum at r = 0.5𝛼 as mass increases. Mass can therefore reach an arbitrarily large magnitude, though not infinite. One consequence of this is that it explains how the universe replenishes (or recycles) its hydrogen.

A neutron star can result from the collapse of a massive star or be the eventual result of the accumulation of a large amount of material at the center of a galaxy. When massive stars with over about 10 solar masses collapse, they leave a very dense core called a neutron star. Its inward pressure due to gravity is so great that it compresses matter to the point where gravity overpowers electromagnetism. Protons and electrons can no longer remain in their electrostatic (atomic) resonance and are forced to combine to form neutrons. (Black holes aside,) neutron stars are the smallest and densest stellar objects known in the universe. In smaller neutron stars, the Schwarzchild radius is within the physical radius of the star (r>𝛼).

As more and more mass accumulates, the neutrons in the star become more and more compressed, though they cannot collapse further, as mentioned above. 

As more and more mass accumulates, the radius of the star increases (as the cube root of mass), but its Schwarzschild radius increases faster (linearly with mass). At a certain point, the Schwarzschild radius increases to be outside the physical radius. When it exceeds the physical radius — when 𝛼>r — it is considered by the standard model to be the event horizon of a black hole. This is because the force of gravity becomes asymptotic when r=𝛼, according to Schwarzschild’s strong field metric. According to the redshift metric, r=0.5𝛼 is where gravitational force reaches its maximum, but it decreases when r<0.5𝛼. As the mass accumulates, 𝛼 gets even larger compared to 0.5r, and gravity becomes weaker because of the degree to which spacetime is being distorted. The centers of neutron stars, like all stars, therefore have extremely high pressures and temperatures, though weak gravitational forces. They instead experience a gravitation attraction towards r=0.5𝛼 and away from the center.

As we saw in the g_z curve (in figure 14 above), as we move closer to the center of mass, gravity becomes weak at r≪𝛼. It, in fact, begins experiencing an increasing gravitational attraction towards r=0.5𝛼 and away from its center. This means that, as the mass of a neutron star increases, it will reach a point where the gravity near its center becomes too weak to maintain the high pressures required to keep compressing the protons and electrons together. They are therefore able to separate again, forming a build-up of hydrogen atoms at the center of the neutron star. This will not occur throughout the volume of the neutron star because, as we move away from its center, gravity increases again.

When the pressure of hydrogen builds up sufficiently, it will begin forcing its way through the shell of the neutron star around it and escaping from its surface at high energies. (While this matter will be mostly hydrogen, it will also contain other heavier elements resulting from nuclear fusion reactions.) These high energy particles will be accelerated towards the highest point in the gravitation field at r=0.5𝛼. When they reach it, they are moving with too much momentum for the gravitational field to stop their outward trajectories. This emission process will continue until the mass of the neutron star decreases to the point where the Schwarzschild radius is within the physical radius.

The more massive the neutron star, the higher the hydrogen pressure in its center, and the more particles and radiation will be released as a result of neutron dissociation. It is suggested by the present model that this is the origin of quasars. The process starts out with masses of hundreds of millions to billions of solar masses and ends when the core has a residual of thousands of solar masses.

Arguably the most controversial result of this model (not to mention an accurate application of Einstein’s General Relativity) is that ‘black hole’ singularities are not physically possible. This is simply because gravity can never be stronger than inverse-square if planetary orbits are observed to precess, a fact that Isaac Newton knew to be true in 1687. In addition, since gravity becomes weaker when r<0.5𝛼, and since neutron stars have no maximum mass, black holes are not needed in order to explain extremely massive objects.

---

 For a selection of video lectures by Dr. Vivian Robinson on this and other topics, click HERE.
For more information about Robinson’s visionary book, click HERE.

BACK TO TOP