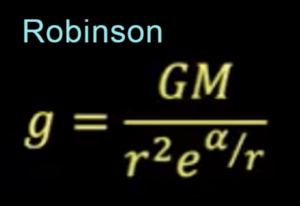Below is a list of scientific terms, some of which emerge from the work of Quicycle members, and others of which gain new nuance as a result of this work. (The definitions relate primarily to physics and chemistry.)
A — B — C— D — E – F – G – H – I – L – M – N – O – P – Q – R – S – T – V – W
A
Absolute Force:
This is not an inter-action. It is just action. It is a force to which there is no resistance, a process that must occur. Example: If there is a changing electric field, there will be a corresponding changing magnetic field associated with it. It is a fundamental process of electro-mass dynamics.
Absolute Relativity Theory:
The conscious restriction of thinking to include only elements with the proper fully relativistic form.
For more detail, see (below) The Mathematics of Absolute Relativity Theory (M.A.R.T.), as well as the Williamson equation upon which it is based.
Acid:
An acid is a substance that releases hydrogen (H+) ions into solution when placed in water. An H+ ion is very reactive, being simply a bare proton, and it will attach itself to an electron-rich oxygen atom on the nearest water (H2O) molecule, forming the H3O+ ion. The stronger an acid, the more H+ ions it produces in solution. Hydrochloric acid (HCl) is a strong acid because it releases all of its hydrogen into solution as H+ ions. A weak acid, like vinegar (HC2H3O2), only releases a small percentage. The exposed proton of the H+ ion is the reason that strong acids can be so corrosive. Each H+ ion is desperately seeking an electron in which to clothe its bare proton nucleus. It does so by taking an electron from another substance around it, which results in a (sometimes violent) chemical reaction.
Alkali:
See Base
Antiferromagnetism:
Antiferromagnetism is a state in which the unpaired electron spins on adjacent atoms in the metallic crystal are anti-parallel to one another. This creates a net spin-zero state for the crystal as a whole, and it will therefore not exert an external magnetic force.
It is proposed that antiferromagnetism is not a form of ferromagnetism, but rather a resonance resulting from an electron-gas coupling.
For more information, see chromium (Cr) or Magnetism & Magnetic Trends.
Antimatter:
A particle of matter has a corresponding antimatter particle (or antiparticle) that has the same mass but the opposite electric charge.
The proton’s anti-particle is the anti-proton, and it has the same mass as the proton but a negative charge. The anti-particle of the electron is the positron, which has positive charge. While neutrons and neutrinos are electrically neutral, they still have anti-particles, called the anti-neutron and the anti-neutrino.
In the case of the neutron, while it has no overall charge, it is comprised of (according to the standard model) quarks that have charge or (according to the rotating photon model of matter) photon harmonic resonances that outwardly express either their positive or negative electric fields. In the corresponding antiparticles, these resonances rotate in the opposite direction, yielding the opposite charge for charged particles but the same overall neutrality for neutral particles.
According to this model, antimatter is matter that is composed of particles whose internal (photon) structure has opposite quantum ‘spin-handedness’ (chirality), which therefore outwardly expresses the opposite polarity of the internal photon’s electric field.
When a particle and its anti-particle meet, they unlock each other’s internal spin angular momenta, converting their rotating photons to linear photons in a high-energy release called a matter-antimatter annihilation. (See this presentation excerpt for a conjecture as to the specific sub-quantum mechanism involved.)
Antimatter is encountered in association with nuclear transmutation reactions. According to the rotating photon model of matter, antimatter arises as a result of a nuclear reaction because antimatter particles are the photon resonances that form (and are consumed) in order to conserve photon angular momentum (as well as other quantum numbers) through a nuclear reaction. These antimatter particles can then be consumed in other nuclear reactions or in annihilation reactions with matter particles. They will therefore not have long-term survivability in a universe made of regular matter.
Atom:
The smallest particle of a pure element. When two or more atoms are bonded together it is called a molecule. All solids, liquids, and gases are made of atoms or molecules. The periodic table of the elements displays all known atoms in order to their atomic number.
Most of the mass of an atom is concentrated in its nucleus, a tiny positively charged central region containing protons and neutrons. This is surrounded by an electron cloud, a region of negative charge that fills the space around the nucleus. The positive charge field of the nucleus is thus cancelled by the negative charge field of the electron cloud around it. The charges are therefore balanced, and this stabilizes the atom by achieving a lowest energy state. Protons, neutrons, and electrons are known as subatomic particles. If electrons are added or removed, the atom will no longer be balanced and will have an overall charge. It is then called an ion.
Atomic Bond:
Substances form when atoms group together. Atoms will only bond (or stick together) to the extent that they are attracted to each other. That attraction is based upon the interactions between atoms — whether their electron shells are eager to gain or lose electrons, whether they are charged ions, or whether they specifically do not want to interact with other atoms. The position of an element in the periodic table — in which column and in which row it is found — gives us clues as to its bonding properties.
On the periodic table: most of the elements (on the left side) are considered metals and elements on the far right side are considered non-metals. The dividing line between them is a diagonal ‘staircase’ of elements that are considered semi-metals or metalloids. These include B, Si, Ge, As, Sb, Te & At (as shown below).
Elements become more metallic in character the further they get from the metalloids towards the left bottom corner of the table, and more non-metallic towards the top right corner of the table. The reason for this is that larger atoms and those with fewer outer electrons will give these (valence) electrons more easily, and smaller atoms with almost-full electron shells will attract electrons the most strongly. The right-most column, the Noble gases, are generally unreactive because they are both neutral and have full electron shells. (See Periodic Trends for more detail.)
The main types of atomic bonds are: covalent bonds, network covalent bonds, metallic bonds, and ionic bonds. Covalent bonds occur between non-metal atoms (ex: H2O). Network covalent bonds occur in non-metal crystals (ex: C in diamond). Metallic bonds occur between metal atoms (ex: bronze, Cu+Sn). Ionic bonds form between ions of opposite charge (ex: salt, NaCl) involving a metal atom and a non-metal atom. This is because the difference in their electronegativities is enough to go from simply sharing a pair of electrons in a (covalent) bond to completely stealing the electron (in Ionic bonds).
There are also other bond-like interactions, attractions between atoms and molecules that are weaker than bonds. These are called intermolecular forces.
Atomic mass unit (amu):
For convenience, the mass of atoms is usually considered in terms of the mass of the proton (or neutron). One amu is the same as the mass of a single proton, which is 1.67×10−27 kg. This is not a very convenient number to work with, so, instead of saying that a helium atom has a mass of 6.69×10−27 kg, it is easier to say that helium has a mass of 4 amu. Atomic numbers are not perfect integers because they really represent the average mass of all the different isotopes of an element.
Atomic number:
This is the number of protons in an atom’s nucleus, and it determines what kind of element the atom is. The periodic table is arranged in order of atomic number.
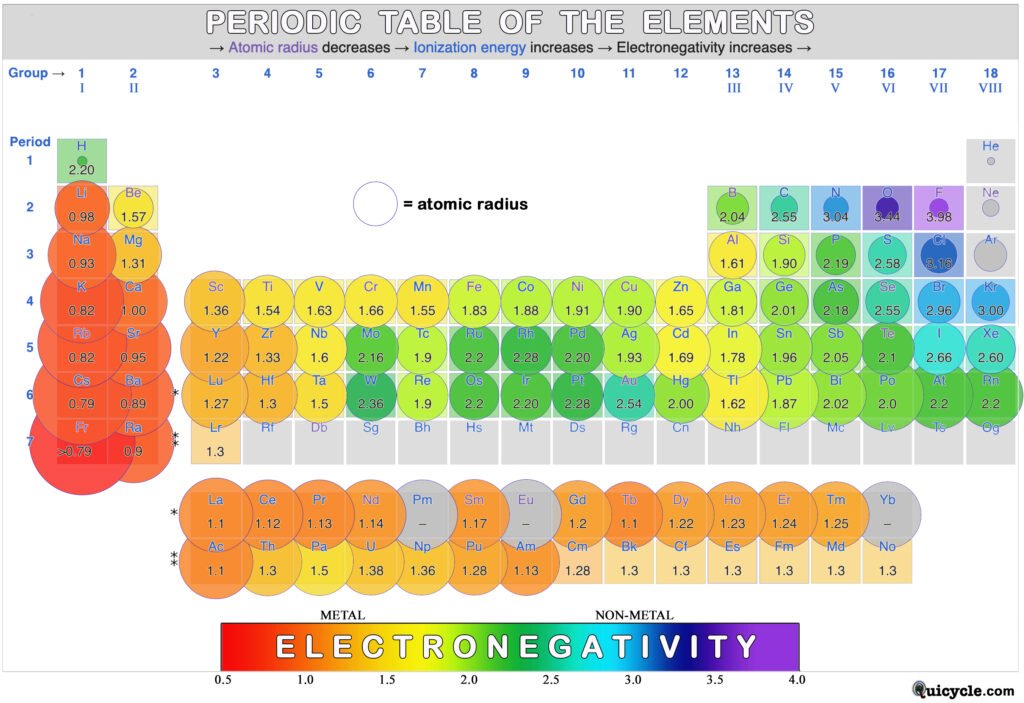
Atomic Radius:
This refers to the size of the atom by referring to the distance from its center to the “edge” of its electron cloud. The “bonding atomic radius” is slightly shorter than the radius of the neutral atom because, when atoms bond, their electron clouds tend to overlap. This makes the radius shorter at that place, and it is calculated by taking half of the bond length — the distance from the nucleus of one atom to the nucleus of the other. The circles in the periodic table below represent the sizes of the atoms when they form covalent bonds. (NOTE: the colors and values in this table represent electronegativity, not size.)
Ionic Radius: When atoms become ions, they gain or lose electrons in order to gain full outer electron shells. This causes their sizes to change because the balance of protons to electrons has changed. This changes the effective nuclear charge. In the case of positive ions, the effective nuclear charge will be greater because there are now more protons than electrons. The inward attraction of the electron cloud towards the nucleus is therefore greater, and positive ions are therefore smaller than their neutral atoms. In the case of negative ions, the effective nuclear charge will be smaller because there are now more electrons than protons. Negative ions are therefore larger than their neutral atoms. Some (metal) ions are capable of making more than one type of ion, for example Germanium (Ge) can make a 2+ or 4+ ion. (This is represented by a 2-tone ion color with more than one charge listed. The larger the charge, the smaller the ion.) Notice that some elements, such as Phosphorus (P) and Sulfur (S), can form positive or negative ions.
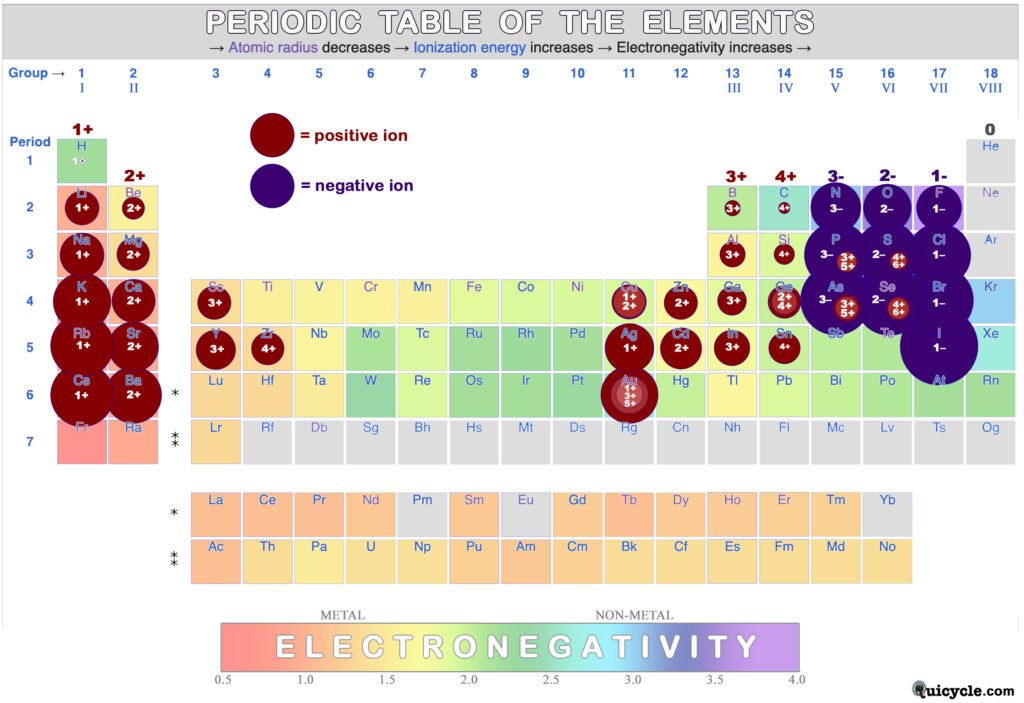
The rainbow color coding (from the previous table) has changed because ions do not have electronegativity values. Ions cannot share electrons in covalent bonds because they have full electron shells. Instead, they simply stick to one another electrostatically in ionic bonds. Notice that the noble gases in group VIII do not form ions because they already have full electron shells, so they will not gain or lose any more. (Kr & Xe can actually bond, but only with the most electrogenative elements like F, O, or Cl. One example is XeF4.)
B
Base:
A base (or alkali) is a substance that attracts and bonds with hydrogen (H+) ions in solution. Most bases are therefore negative ions, like hydroxide (OH–) or hydride (H–), or else they contain atoms with exposed di-electrons (lone pairs), like nitrogen, because these negative charge centers strongly attract positively charged H+ ions.
Body-centered cubic (BCC) structure:
This is a crystal structure defined by a unit cell that has 8 (white) atoms at the corners of a cubic structure, and with one more (blue) atom at its center. Each atom therefore has 8 nearest-neighbor atoms.
BCC structure is slightly less dense of a crystal packing than hexagonal close-packing (HCP) or face-centered cubic (FCC) structure (which is also known as cubic close-packing (CCP)).
Bond:
See atomic bond.
Boson:
A subatomic particle (or quantum state) with an integer quantum spin, meaning a spin of S = 0, 1, 2, etc. All subatomic particles are either a boson or a fermion. Examples of bosons include di-electrons (Cooper Pairs) and photons of light.
The nucleus of the helium atom could then be considered a di-boson state, since it contains a spin-up and spin-down proton and a spin-up and spin-down neutron, thereby balancing overall spin to zero. When the spin-zero di-electron shell is added to form the helium atom, it can similarly be considered a highly stable tri-bosonic state.
C
Charge:
Charge results from an imbalance in electric field energy. It can have a positive polarity or a negative polarity. Like polarities repel one another due to the energy increase associated with the constructive interference of electric field energy; opposite polarities attract due to the energy lowering associated with the destructive interference of electric field energy.
The charge of the electron results from its internal topology. As a result of the geometry of this double-loop torus and the circular polarization of the photon, the photon’s negative electric field is pointing outwards at all times, which is what gives the electron its negative monopole charge. An electron is a fermion and has a left-handed spin of ½ℏ, a charge of -1.6×10-19 Coulombs, and a mass-energy content of 511 keV.
For more on electrons, see Understanding electrons.
For more on how the electron charge can be calculated, a priori, based upon the Williamson/van der Mark model of the electron, see Calculating The Electron Charge.
Chirality:
Chirality means that the mirror image of an object cannot be superimposed exactly upon it. The most common example is ‘handedness,’ meaning, a left-handed form versus a right-handed form. Human hands are chiral, and we often use the left- versus right-handedness to differentiate between orientations in both physics and chemistry.
This is particularly relevant to rotational directions for objects that are spinning, such as a planets or charged subatomic particles, because they have an equatorial rotational direction that corresponds to a north-south axis of magnetization.
The electron is proposed to be a topology made up of a photon double-loop rotation. If the instantaneous magnetic axis through the toroidal structure has the north pole pointing upward — the thumb direction in a left-handed thumbs-up — then the toroidal flow must be left handed with respect to that north pole — the rotational direction in which the fingers are curled and pointing — in order for charge to be negative. A right-handed chirality will yield the same flow, but with a positive charge. That particle is called a positron.
Compton Wavelength:
This is the wavelength (λC) of a photon that has the same energy as represented by the rest mass/energy of a subatomic particle. The equation that represents this relationship is λC=h/mc. The Compton wavelength is inversely proportional to the mass of the particle, so larger particles have smaller Compton wavelengths. (Compare: De Broglie wavelength)
Covalent bond:
Covalent bonds occur between non-metal atoms (ex: H2O). Non-metals occupy the right-side columns of the periodic table, and they represent atoms with high electronegativity that strongly attract electrons because they want to complete their almost-filled electron shell. When two non-metal atoms encounter each other, neither will therefore be willing to relinquish an electron. They are therefore forced to share electrons. That way, neither atom feels like it has lost an electron but both feel like they have gained one (or more).
Curie Temperature (Tc):
The temperature at which a ferromagnetic metal loses its permanent magnetization. This occurs because there is so much thermal entropy at this temperature that the ferromagnetic spin bonding between unpaired electrons on adjacent atoms are disrupted.
(See the magnetic properties of iron for more details.)
D
De Broglie Wavelength:
(Pronounced: De-Broyi) This is the wavelength (λB) of a photon that represents the classical momentum of a subatomic particle. The equation that represents this relationship is λB=h/p, where its momentum p=mv. Thus, the larger the momentum (i.e. its mass and/or velocity), the shorter the De Broglie wavelength. An electron in a matter state that occupies a larger volume will have a larger De Broglie wavelength. (Compare: Compton wavelength)
When a quantum particle gains energy, perhaps via acceleration, its De Broglie wavelength decreases. When it loses energy, perhaps via field cancellation, its De Broglie wavelength increases. This can be seen when the hydrogen (H) atom forms from an isolated proton and electron. (A useful analogy might be the spinning figure skater who spins faster when they draw their arms in closer to their axis of rotation — their body.)
Degenerate:
While the term can certainly be used to describe human behavior, in chemistry and physics, the term is used to describe the equivalent energy state of two or more electrons. It means that they have the same spin and that they occupy the same orbital (sub-shell).
Diamagnetism:
This is when a substance is repelled from a magnetic field because it contains paired electrons. These paired electrons are in a state of field cancellation with one another. The presence of an external magnetic field will disrupt the coherence of this di-electron state, raising its energy. This causes it to repel away from the field in search of a lower energy state. Copper (Cu) and zinc (Zn) are diamagnetic. (See Magnetism for more detail.)
Di-electron:
A pair of electrons of opposite spin that have completely superimposed upon one another. This yields a single, coherent, quantum state which brings their magnetic fields into equal and opposite orientations at every point within the di-electron, facilitating almost total magnetic field cancellation. It also facilitates a cancellation of the equal and opposite quantum spins, converting two fermions (with spin ½ℏ) to one boson (with spin 0). This results in a highly stable and favorable state, in spite of the like-charge electric field repulsion, because it allows for a significant lowering of energy. Examples of di-electrons include the 1s2 shell in helium (He), the covalent bond in the hydrogen molecule (H2), the “lone pair” on the nitrogen atom (N), and the superconducting Cooper pair. For more on electrons, see Understanding electrons.
Dipole-dipole force:
When a molecule features a covalent bond between atoms of two different elements, their different electronegativities can cause them to share the bonding electrons unequally. The atom that pulls more electron density to its side of the bond will manifest a slight negative-charge bias — a partial charge — and the one that loses some of its electron density from its side of the bond will manifest a slight positive-charge bias. This makes the molecule polar. Polar molecules are also called ‘dipoles’ because they have two opposite ‘poles’ or charge biases on opposite ends of the molecule. This will cause these opposite partially charged ends on adjacent molecules to attract each other. This attraction is not as strong as an actual atomic bond.
Dispersion force:
See London Dispersion Force.
E
E=mc2:
This is Einstein’s famous formula that relates energy (E) to mass (m), using the square of the speed of light (c2) as the ratio (or conversion factor) between them. (See relativity) Radiant energy and matter are really two forms of the same root-energy ‘stuff.’ If we want to know how much pure energy we get if we convert matter into pure radiant energy, we multiply the mass by the speed of light squared, which is a very large number (9×1016). It also reflects the fact that particles that have mass, such as electrons (see below), are photons of light that are traveling in a circle (or knot) rather than in a straight line. Such self-sustaining photon resonance structures are the essence of matter.
Mass can also be expressed by rearranging this equation as m=E/c2. This implies that whatever has energy, has (inertial) mass, and it can be expressed in units of E/c2.
Effective Magnetic Electron (EME) Count:
When a metal atom in a metallic crystal contains 2 or more unpaired core electrons, their geometry can bring their spins and magnetic fields to interact in such a way that results in overall spin reduction and magnetic field cancellation through destructive interference. It is proposed that this will have the effect of lowering the overall magnetic signature of these electrons, as they relate to an external magnetic field. This, in turn, will dictate the strength of a metal’s paramagnetic response — its magnetic susceptibility (χm) value. This appears to account for why, for example, titanium (Ti) has about half the paramagnetic strength as scandium (Sc), even though it has twice the number of unpaired electrons.
Effective Nuclear Charge (Zeff):
The protons in the nucleus attract the electrons in the electron cloud around it. The more protons in the nucleus and the more electrons in the orbitals, the more strongly the two are attracted towards each other. This shrinks the size of the atom. In general, effective nuclear charge increases as we move to the right in a row on the periodic table, since we are adding both protons and electrons when we move to the next element. This means atoms get smaller as we move to the right in a row on the periodic table. In general, effective nuclear charge decreases as we move down a column (group) on the periodic table, since we are adding electron shells. The outer electrons are further from the nucleus, which both decreases their attraction to it, and the new shell adds diameter to the atom.
Electric field space:
When dealing with electric field, in the mathematics of absolute relativity theory (MART), it is dealt with differently from magnetic field or spin, for example. Electric field is a bi-vector quantity, a differential involving 1 dimension of space and 1 dimension of time. (see spacetime.) Electric field is a directed 2-dimensional space-time plane element (Ξ0i) in M.A.R.T.
It is useful to refer to this mathematical construct as electric field space, even though it is nothing more than a subset of normal 4-dimensional spacetime. (See momentum space for more detail.)
Reference:
J.G. Williamson, A. Benn, M. Mercury, ‘Quantum Spin In 4 Derived 3-Spaces’, Quicycle Journal, 2022.
Electric permittivity (ε0):
See Spacetime
Electromagnetic radiation:
The scientific term for light waves, whether they are in the visible part of the spectrum (like the colors of the rainbow) or the invisible part of the spectrum (for example radio waves or gamma rays).
Light waves store part of their energy in an electric field and part of it in a magnetic field, hence the name. In a typical circularly-polarized photon, the electric and magnetic fields spiral around the axis of travel, 90 degrees apart. Since an electric field incites a forward motion, like velocity, and magnetic field incites a rotation (see spacetime), the combination of the two should yield a combined electromagnetic field that spirals as it moves forward. Electromagnetic waves can only travel at the speed of light (c), which is just under 300,000 kilometers per second.
By analogy, whatever bulk water is or is not, it has the property that energy waves can propagate along its surface as water waves. Similarly, whatever spacetime is or is not, it has the property that photons of electromagnetic energy can travel through it as waves (of field differentials). Like most waves, electromagnetic waves have a wavelength (𝜆) and a frequency (𝜈), and the mathematical relationship between these three properties is given by the equation c=𝜆𝜈. This implies that the larger the frequency, the smaller the wavelength, and vice versa, because the speed of light (c) must remain unchanged.
The amount of energy carried by an electromagnetic wave depends on its frequency. This is reflected in the Planck equation for energy, E=h𝜈, in which the higher the frequency (𝜈) of the wave, the more energy (E) it carries. The ratio between energy and frequency is Planck’s constant (h) (where h=6.626×10-34 m2kg/s). High frequency waves, such as ultraviolet waves, are more dangerous than low frequency waves, such as radio waves, because UV waves carry much more energy. They can therefore ionize molecules, disrupt cellular function, or cause radiation burns. From lowest energy to highest, the main types of electromagnetic radiation are: radio, microwave, infrared, visible (red/orange/yellow/green/blue/indigo/violet), ultraviolet, X-ray, gamma ray.
Electron (e–):
One of the three subatomic particles out of which all atoms are made. (The other two are the proton and the neutron.) An electron is negatively charged and highly stable.
Contrary to popular misconception, it is not a point particle but it has a sub-structure that gives rise to its properties. It is made of a single photon of light making two revolutions per wavelength. An electron is thus a self-confined knot of concentrated light energy traveling around itself at the speed of light. It has a toroidal (donut-shaped) sub-structure in (momentum) space, but the charge field of an isolated electron (or an s-orbital electron around a hydrogen or helium atom) manifests as a sphere (below, right) in electric field space. The diagram below represents the 3 components of the electron’s internal quantum spin. (See spin.)
The charge of the electron results from its internal topology. As a result of the geometry of this double-loop torus and the circular polarization of the photon, the photon’s negative electric field is pointing outwards at all times, which is what gives the electron its negative charge. An electron is a fermion and has a left-handed spin of S=½ℏ, a charge of C=-1.6×10-19 Coulombs, and a mass-energy content of 511 keV. For more on electrons, see Understanding electrons
.
References: J.G. Williamson, M.B. van der Mark, ‘Is The Electron A Photon With Toroidal Topology?’, Annales de la Fondation Louis de Broglie (1997) J.G. Williamson, ‘A New Linear Theory Of Light And Matter’, J. Phys. (2019) 
J.G. Williamson: Unifying the electron’s particle and wave natures
Electron affinity:
This is a measure of how much an atom wants to accept another electron. It is a measure of how much an added electron would stabilize the atom, so it is quantified by how much energy is released when an electron is added. The more negative the energy value, the more the atom wants another electron. Atoms like chlorine (Cl) and fluorine (F) have the largest negative values. If the value is positive, it indicates that the atom’s orbital resonance is so stable that an added electron would be unfavorable and would increase energy. Examples include noble gases, like neon (Ne), or atoms with a full orbital, like zinc (Zn).
Electron volt (eV):
Even though electron volts (eV) sounds like a unit of electrical potential — like the volt (V) — it is actually a measure of energy, which is usually measured in S.I. units of joules (J). Electron volts can express kinetic energy (of movement) or even internal mass energy, as in E=mc2. (Mass can therefore be expressed by the equation m=E/c2 , and its value is often reported in units of eV/c2.)
An energy of 1 eV is equivalent to an energy of 1.609 x 10-19 J. This number is convenient because the 1 electron has a charge of 1.609 x 10-19 C.
Particles with high energy or traveling at high velocities might express energy in the keV, MeV, or even GeV range. The electron has a mass/energy of
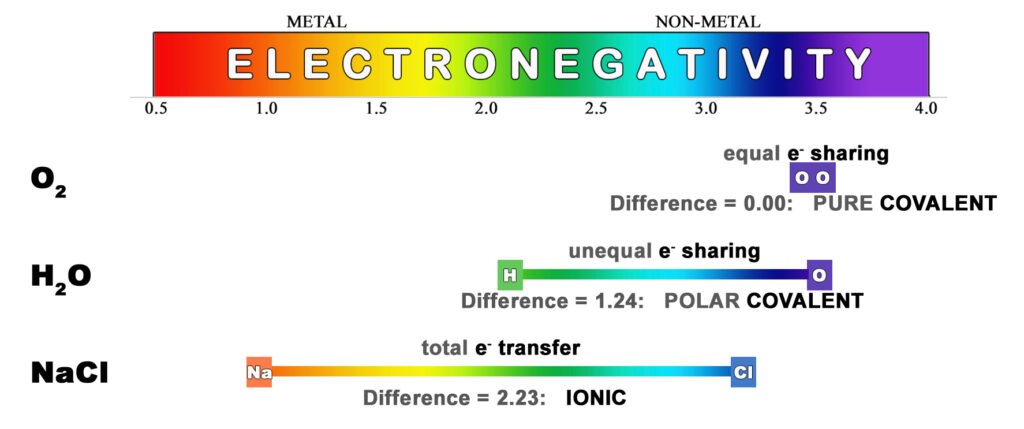
Electronegativity (χe):
When two atoms bond, electronegativity is a measure of how strongly an atom‘s nucleus pulls the bonding di-electron toward itself. When there is an electronegativity difference between the two bonding atoms, the more electronegative atom will pull electron density more strongly, resulting in an imbalance in the electron sharing. This results in a polar bond. In general, as we move across the periodic table, the atoms get smaller. This is due to the stronger pull from the nucleus (effective nuclear charge) since it is closer. Therefore, the smaller the atom, the higher its electronegativity. As we move down the periodic table, atoms get larger due to having additional electron shells. This lowers electronegativity because the outer electrons are not as strongly held to the atom. Fluorine (F) has the highest electronegativity on the periodic table and francium (Fr) has the lowest. In the rainbow-colored diagram below, red represents the lowest electronegativity and violet represents the highest. The circles represent the sizes of the atoms (atomic radius) when they form covalent bonds.
Element:
A unique, pure substance made up of only one type of atom. The number of protons in an atom’s nucleus determines which element it is, and this is known as its atomic number. The periodic table of the elements lists all 118 known elements in order of their atomic numbers. By way of example, the nuclei of all hydrogen atoms contain 1 proton, all helium nuclei contain two, and so on. The uranium atom has the heaviest naturally-occurring nucleus, and it contains 92 protons. All of the heavier nuclei, from atomic number 93 through 118, do not occur naturally and are created through the application of man-made nuclear technologies (like reactors, for example). They are all naturally unstable, and therefore, radioactive.
Energy:
Most broadly, energy is the ability to do work or to transfer heat. The S.I. unit for energy is the joule (J), but there are many other familiar units in which energy can be measured, such as calorie, electron volt, or BTU.
According to the 1st Law of Thermodynamics, energy is conserved. It can neither be created nor destroyed; it can only be transformed from one form into another. As an example, a battery works by converting chemical energy from the batteries ingredients into a flow of electrical potential by causing electrons to be transferred from one place or substance to another. In doing so, the battery’s ingredients are changed (or spent) by the loss (or gain) of this electron density.
Another important example is that electromagnetic energy can be converted between its photon form and its mass form according to Einstein’s equation, E=mc2.
According to the sub-quantum mechanics approach, matter is made up of photons, which means that both photons and particles are ultimately electromagnetic fields (and field topologies) that can also carry angular momentum (spin). The mathematics of this approach (M.A.R.T.) therefore considers each of these field and spin elements at the level of field — at the level of root-energy, as seen in the Williamson equation.
F
Face-centered cubic (FCC) structure:
This is a crystal structure defined by a unit cell that has 8 (white) atoms at the corners of a cubic structure, and 6 more (blue) atoms at the center of each face. Each atom therefore has 12 nearest-neighbor atoms.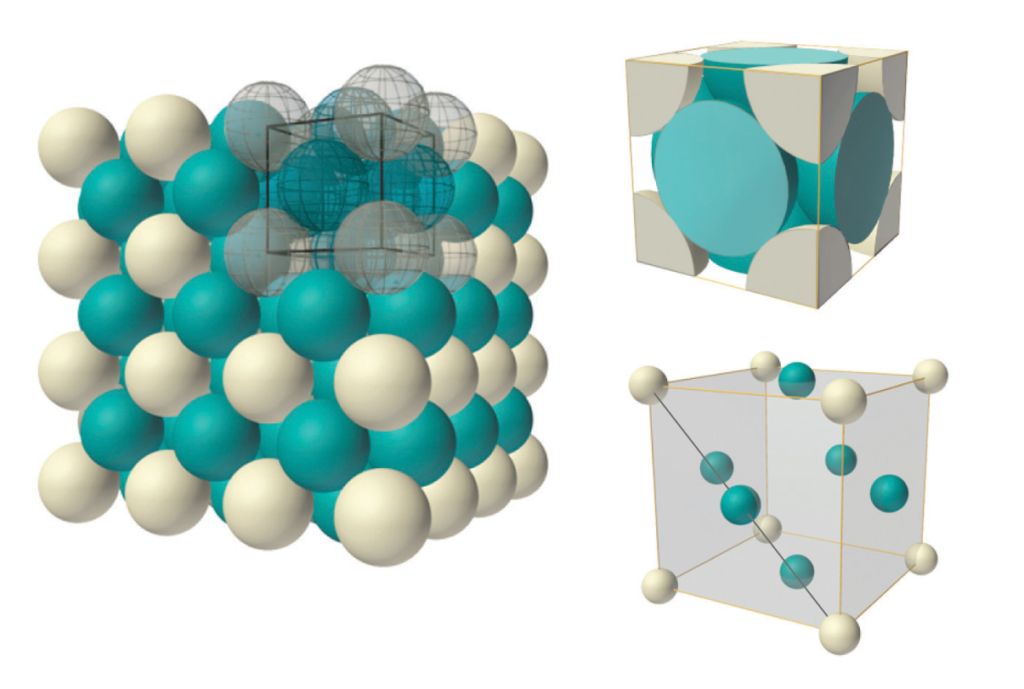
Both FCC structure and hexagonal close-packing (HCP) have denser crystal packing than body-centered cubic (BCC) structure.
Fermi surface:
In solid state physics, when the atoms in a crystal are in their lowest energy state, the Fermi surface is a geometric surface (in momentum space) that divides between regions in which electrons can be found versus those in which they cannot. The Fermi surface is closely related to the structure of the crystal lattice, as well as the electron energy bands within it.
As a result, the Fermi surface is highly relevant to any properties that rely on electron resonances or mobility within a crystal. These include electrical, magnetic, optical, and thermal properties. (Click here for more information.)
The following images of the Fermi surface of copper (Cu) were obtained by Weber (et.al.) using a process known as 2D-ACAR [ref].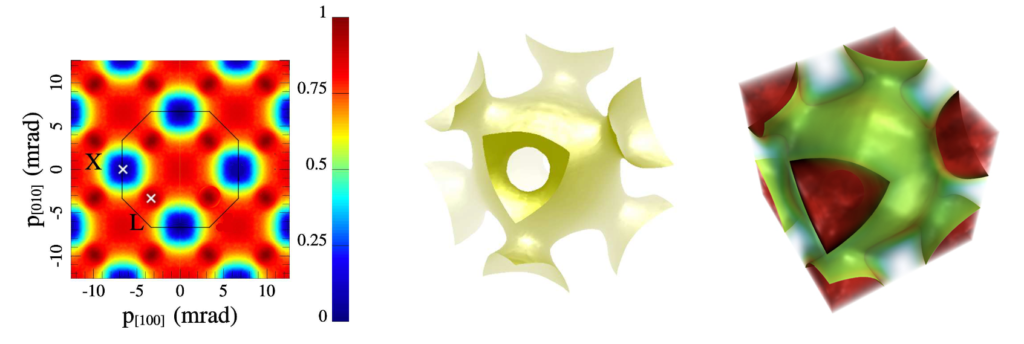
This structure may bear out the proposed structure for copper: a pd-hybridized cubic 3rd shell.
Additional images of Fermi surfaces, calculated using the standard model’s density functional theory (DFT), can be found here.
Fermion:
A subatomic particle with an odd half-integer (½ℏ) quantum spin, meaning a spin of S = 1/2, 3/2, 5/2, etc. All subatomic particles are either a fermion or a boson. Examples of fermions include the electron, proton, and neutron.
Ferromagnetic spin bonding (FSB):
This is a spin-mediated mechanism that is proposed to explain the ferromagnetism of iron (Fe), cobalt (Co), and nickel (Ni). It involves two primary aspects: (1) the symmetrical electron geometry of the pd–hybridized orbitals of the transition metals, and (2) the constriction and extension of the unpaired electron orbitals due to di-electron repulsion. It is proposed that this brings unpaired electron orbitals into close enough association to facilitate spin bonding.
See Magnetism or iron for more detail.
There are other forms of spin bonding, such as parallel spin bonding, linear spin bonding, partial di-electron inclusion,as well as that responsible for the formation of the di-electron — total di-electron inclusion.
References: A. Benn, J.G. Williamson, ‘pd-Hybridization And The Electron Geometry Of Fluorine, Neon, And Iron,’ Quicycle Journal, 2024 A. Benn, J.G. Williamson, ‘The Photonic Topology Of Quantum Spin’, Quicycle Journal, 2022. Arnie Benn: The Physics Of Sub-Quantum Spin, followed by this Q&A.
Ferromagnetism:
This is when a metal, after being exposed to an external magnetic field, can retain its internal magnetic field alignment after the external field is removed. It can therefore act as a permanent magnet. When exposed to an external magnetic field, the unpaired electrons throughout the substance align with the field, and when the field is removed, the electrons are able to maintain their alignment as a result of interactions with one another. Iron (Fe), cobalt (Co), and nickel (Ni) are ferromagnetic. Most other metals are paramagnetic, which means they only hold their magnetic alignment in the presence of an external magnetic field. Without it, their unpaired electrons revert back to random alignments.
Using the deeper understanding of electrons and their interactions revealed in sub-quantum mechanics, it is here proposed that the mechanism of ferromagnetism arises from two specific contributing factors: (1) the pd-hybridized electron domain geometry, and (2) the interactions between extended orbital lobes within the 8-directional 3rd-shell electron geometry. For example, cobalt and manganese share the same electron domain geometry, but cobalt is ferromagnetic while manganese is only paramagnetic. It is here proposed that the reason for this is that manganese only shares the geometric factor. It does not have the appropriate orbital interaction factor, which cobalt does.
See Magnetism or iron for more detail.
References: A. Benn, J.G. Williamson, ‘pd-Hybridization And The Electron Geometry Of Fluorine, Neon, And Iron,’ Quicycle Journal, 2024 CLICK HERE to watch a possible explanation of the physical mechanism behind ferromagnetism, on the Demystify Sci podcast.
Field cancellation:
When opposite electric field polarities encounter each other, they cancel each other out (as the sum of opposite bi-vector quantities). This lowering of electric field energy results in a force of electrostatic attraction. When like electric field polarities encounter each other, the increase in electric field energy results in a repulsive force.
The same concept can be applied to magnetic field energy, where ‘north’ and ‘south’ polarities field-cancel and attract while like polarities repel.
It is here proposed that the same is also true of sub-quantum spin, where these interactions of photonic angular momentum phase topologies can either raise or lower overall energy.
Fission:
Nuclear fission is the process whereby an atom‘s nucleus splits, yielding two smaller nuclei (and thus, two new atoms) and a large amount of energy.
The most famous cases of fission involve uranium (U) and plutonium (Pu), since the first atomic weapons employed these elements in their radioactive cores.
Frequency (𝜈):
The frequency of a wave is a measure of how frequently it passes a given point each second, or put another way, how many wave crests pass a given point each second. If two waves pass every second, the frequency is 2 (waves) “per second,” also known as 2 Hertz (Hz). Frequency is measured in “per second,” which means 1/sec (or s-1). This means that frequency is the inverse (or reciprocal) of time, which is measured in sec/1 (or s1). Frequency represents energy. As reflected in the Planck equation, E=h𝜈, the higher the frequency (𝜈) of an electromagnetic wave, the more energy (E) it carries. (Planck’s constant h = 6.626×10-34 m2kg/s.) High frequency ultraviolet waves are more dangerous than low frequency radio waves because the UV waves carry much more energy. With electromagnetic (light) waves, when frequency (𝜈) increases, wavelength (𝜆) decreases, and vice versa. This is because the speed of light (c) is constant, and the three are related by the equation c=𝜆𝜈. Frequency is also the means by which we measure time, whether the frequency of a pendulum, an atom, or a planetary orbit. Without frequency, there is no time measurement.
Fusion:
Nuclear fusion is the process whereby the nuclei of two small atoms combine, yielding one larger nucleus and a large amount of energy.
The most famous case of fusion involves the combination of hydrogen (H) atoms to form helium (He), as is believed by many to be the nature of stellar fusion.
G
Gravity (G):
Gravity is a very weak force exerted by one mass upon another. In fact, it is about 1038 times weaker than electromagnetism. Isaac Newton’s equation for gravity is F=GMm/r2. This equation describes that the force (F) of attraction exerted by one mass (M) upon another mass (m) gets weaker with (the square of the) distance (r). (The gravitational constant G=6.674×10−11 m3kg−1s−2.)
Albert Einstein amended Newton’s gravity in his General Theory Of Relativity (GTR). Interestingly, Einstein’s field equations in GTR do not represent an equation for the force of gravity. They only express the difference between GTR and Newtonian gravity. We can therefore use it to updated Newton’s force equation, which becomes F=GMm/(1+𝛼/r)r2, where 𝛼=2GM/c2. (See Robinson, 2021)
Einstein proposed that gravity is caused by mass distorting spacetime, but he provided no explanation as to the mechanism of that distortion or the precise nature of spacetime.
According to the latest model of gravity by Vivian Robinson, the mechanism by which mass distorts spacetime is via the redshift of photons. (See more detail here.)
According to the Robinson Model of Sub-Quantum Gravity, gravity results from the quantum properties of subatomic particles. (See sub-quantum mechanics.) Gravity is caused by a change in the refractive index of space, which is caused by the radial differential of the electric permittivity of space. In turn, this is induced by the high frequency electric field oscillations resulting from the rotating photon structure of protons and neutrons. The high frequency nucleon oscillations add to produce a variation in electric permittivity that produces the same deflection for photons of all frequencies.
This approach results in a single, simple equation — an equation of sub-quantum gravity: Fz=GMm/r2e𝛼/r where 𝛼=2GM/c2
This equation derives Newton’s inverse square law as a first approximation, Einstein’s field equations as a second approximation, and the bright torus-shaped accretion disc observed (at r=0.5𝛼) around massive objects and galaxy centers as an exact solution. Under this “redshift” metric, gravity can never reach infinite magnitude. It reaches a maximum when r=0.5𝛼, and then decreases towards the center of the extremely massive object.
Gravity is therefore an electromagnetic effect. When mass distorts spacetime strongly, the force of gravity is weakened to slightly less than inverse-square. That is the reason the orbit of Mercury’s perihelion precesses around the Sun in its direction of travel. (If gravity were stronger than inverse-square, such orbits would regress.)
Robinson summarizes gravity as follows:
“Mass does not distort space-time to produce gravity. Gravity is caused by mass increasing the electric permittivity of the space surrounding it. The changed permittivity redshifts and deflects photons, in the same manner as is known for gravity. Space-time distortion, i.e., photon redshift, is the result of gravity, not its cause.”
References: Physical Explanation of Einstein’s Gravity, J. Phys. Commun. 2021 Vivian Robinson: Visualizing Sub-Quantum Gravity, followed by this Q&A
H
Harmonic resonance:
When an object vibrates or when waves interact, if their frequencies are multiples of one another then some of their nodes can overlap perfectly where they meet. The waves then reinforce each other and stabilize themselves into a single symmetrical wave state. Such a harmonic resonance state represents a lower energy state for a system since the waves can now share energy. They will therefore naturally seek out this state if they can. One example of a harmonic resonance would be the wave state set up on a guitar or a violin string when they are played, since multiple harmonics are sounding simultaneously, their waves superimposed along the string. Another occurs when a wine glass is shattered by a sound wave whose resonance matches perfectly with its interior volume. If the sound wave carries enough power, the vibrations it induces in the glass structure can destabilize it, causing it to crack or shatter. Subatomic particles like protons or electrons are also harmonic resonance states involving the rotating photons of various energies that make them up. Overall, quantum states can only be stable and coherent if they are in a state of harmonic resonance. Since there are no stable states between harmonics, it means that harmonic states will be intrinsically quantized. Mathematically, the term ‘harmonic’ means that the wave equations satisfy the double differential of themselves (where ∇2=0).
h-bar (ℏ):
This is the reduced Planck’s constant, obtained by dividing Planck’s constant (h) by the circumference of the unit circle (2π).
See Planck’s constant (h)
Hexagonal close-packing (HCP) structure:
This is a crystal structure containing hexagonally-packed, planar layers of atoms that stack upon one another in such a way that allows atoms of one layer to nestle in between the atoms of the adjacent layer. This allows for the densest form of atomic packing in which each atom has 12 nearest-neighbor atoms.
There are two forms of this stacking that typically occur: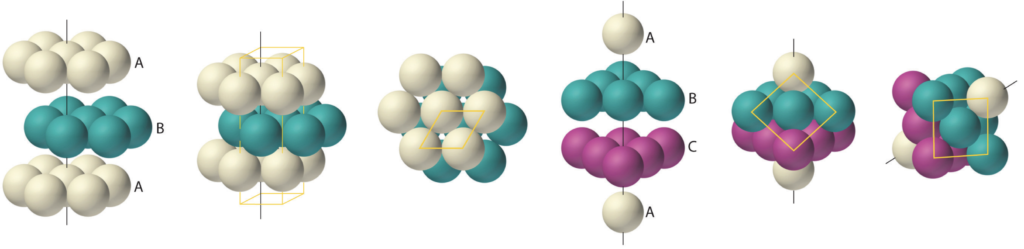
Hexagonal close-packing (HCP): (shown on the left above)
In this form, every other layer has the identical offset; every other layer has its atoms exactly vertically above (or below) each other. This is referred to as ABA form (as shown by the white A layers and the blue B layer above, left).
Cubic close-packing (CCP): (shown on the right above)
This is also commonly known as face-centered cubic (FCC) because, when viewed at a different angle, the hexagonal layers appear to form a cubic structure. In this form, every A layer is followed by first one offset, a B layer, and then the other, a C layer. In this form, every third layer has its atoms exactly vertically above (or below) each other. This is referred to as ABC form (as shown by the white A layers, blue B layer, and purple C layer above, right).
Body-centered cubic (BCC) structure has a slightly less dense crystal packing than hexagonal close-packing (HCP) or face-centered cubic (FCC), and only 8 nearest-neighbor atoms for each atom in the crystal.
Hilbert’s 6th problem:
In 1900, David Hilbert published a list of 23 problems in mathematics that were unanswered at the time. One of the two that remain to be solved is Hilbert’s 6th problem — the “Mathematical treatment of the axioms of physics.” It seeks a single mathematical approach that underpins all of the axioms and laws of physics.
We, in Quicycle, believe that the Mathematics Of Absolute Relativity Theory (M.A.R.T.), encompassed by the fully relativistic Williamson equation, is a bold step in the right direction. It extends relativistic quantum mechanics into the realm within subatomic particles, and we therefore like to call it sub-quantum mechanics.
Reference: J.G. Williamson, Absolute Relativity Theory: A Proposed Solution To Hilbert’s 6th.
Hedgehog:
The directed space-space-space volume element (Ξ123) in M.A.R.T. The element can be outwardly-directed, like the spines on a hedgehog, or — a somewhat less comfortable image (for the hedgehog) — inwardly-directed.
Hund’s 2nd Rule:
According to the second of Hund’s Rules, when unpaired, degenerate electrons share the same sub-shell within an atomic orbital structure, their energy is lowest when their collective spin is maximized. This means that, if an atom has three unpaired electrons in its 2nd shell, as does the nitrogen (N) atom, the lowest energy, most stable state will occur when those three electrons have the same spin and are aligned magnetically parallel to one another. (See Parallel spin bonding)
An explanation as to the physical mechanism behind this ‘principle’ has been proposed by Benn and Williamson.
Reference: J.G. Williamson, A. Benn, M. Mercury, ‘Quantum Spin In 4 Derived 3-Spaces’, Quicycle Journal, 2022. A. Benn, J.G. Williamson, ‘The Photonic Topology Of Sub-Quantum Spin’, Quicycle Journal, 2022. Arnie Benn: The Physics Of Sub-Quantum Spin, followed by this Q&A.
Hybridization:
When different orbitals in the same electron shell, like an s-orbital and a p-orbital, resonate together since they are occupying the same volume of space. This combination of their electron densities changes their shape in order to achieve greater symmetry, stability, and therefore, lowest energy. (See Understanding Electrons: Hybridization for more detail.)
Boron (B) is the first element on the periodic table that experiences hybridization of its electron shell. For a form of hybridization that has been proposed here in order to account for various magnetic properties of the transition metals, see pd-hybridization.
References: A. Benn, J.G. Williamson, ‘pd-Hybridization And The Electron Geometry Of Fluorine, Neon And Iron’, Quicycle Journal, 2024.
Hydrogen ‘bond’:
A hydrogen bond is a dipole-dipole force that is particularly strong. Since it involves a hydrogen (H) atom, and since it is the strongest of the intermolecular forces (see bonds), it is referred to as a hydrogen bond. It is not a bond, however, but rather a meaningful electrostatic dipole attraction. The reason its polarity is so strong is because the hydrogen atom is bonded to either nitrogen (N), oxygen (O), or fluorine (F), the three most electronegative atoms on the periodic table. As such, when they bond with hydrogen, they pull so much electron density from it that it creates a very strong dipole. These strong dipoles then interact with one another strongly, and as a result, they have many important chemical properties. Examples include water (H2O), ammonia (NH3), hydrofluoric acid (HF), or the A-T & G-C connections holding DNA’s double helix together. As such, without hydrogen bonding there would be neither liquid water at room temperature on Earth, nor DNA-based life forms to take note of the fact.
I
Inter-action:
The consideration of a complete quantum system, including source, observer, and that which is common between them.
Intermolecular Forces (IMF):
Intermolecular forces are forces of attraction that exist between noble gas atoms or covalently bonded molecules. There are three forms of IMF attraction, based on the types of atoms or molecules involved, and they are generally not as strong as bonds. The main types of intermolecular forces that hold atoms or molecules together are: London dispersion forces, dipole-dipole attraction, hydrogen ‘bonding’, and ion-dipole attractions.
Inversion:
See Quantum inversion.
Ion:
An atom that has either lost or gained one or more electrons. This means there is no longer a balance between the positive protons in the nucleus and the negative electrons enveloping it. The atom therefore has an overall charge. If it lost electrons it will be a positive ion (also known as a cation). If it gained electrons it will be a negative ion (also known as an anion).
In nature, crystals (like salt or quartz) are made of ions. While the term can refer to either positive or negative ions, it is often used to refer to positive ions, as in the case of cosmic rays, for example. Electromagnetic radiation that has enough energy to knock electrons free from atoms is called ionizing radiation. This also makes it hazardous to biological tissue, since changing the charge of a molecule in the body will affect the chemical role it plays.
Ion-dipole force:
When a polar and covalently bonded molecule encounters an ion, there will be an attraction between them that will usually be stronger than a dipole-dipole attraction, given that an ion involves a full charge rather than the partial charge of a polar molecule. An example is salt water. When salt (NaCl) is exposed to water (H2O) molecules, which are strongly polar (see hydrogen bonding), the attraction between them causes the salt ions to become separated from the solid salt crystal. This process is called dissolving, and a salt solution is formed.
Ionic bond:
Ionic bonds occur between metal and non-metal atoms (ex: NaCl). Metals (like Na) occupy the left-side columns of the periodic table, and they represent atoms with low electronegativity that are willing to relinquish one or more outer electrons in order to reach the stability of a full electron shell. Non-metals (like Cl) occupy the right-side columns, and they represent atoms with high electronegativity that strongly attract electrons because they want to complete their almost-filled electron shell. When a metal and a non-metal atom encounter each other, the non-metal will take one or more electrons from the metal. Both therefore achieve the stability of full electron shells, but, since they are charged, they stick together because of their opposite electric charges.
Ionic Radius:
See atomic radius.
Ionization Energy:
This is the amount of energy needed to remove an electron from an atom, to overcome the attraction from its nucleus. (An analogy might be giving a rocket enough thrust to escape a planet’s gravity.) The higher the ionization energy, the harder it is to remove the electron. The lower the ionization energy, the easier it is to remove the electron. The most reactive elements will be those with either low or high ionization energies. This is because they will either be eager to donate an electron or steal an electron (respectively) in a chemical reaction.
In general, ionization energy increases as we move to the right in a row on the periodic table, since effective nuclear charge is increasing (see above). In general, ionization energy decreases as we move down a column (Group) on the periodic table, since the valence electrons are further from the nucleus and therefore less strongly attracted to it.
Isotope:
Atoms of the same element that have different masses are called isotopes. An element is defined by how many protons it contains in its nucleus. But it can have varying numbers of neutrons, which changes its mass but does not affect its charge because neutrons are neutral. By way of example, the three hydrogen isotopes are 
protium (1H1), 
deuterium (1H2), and 
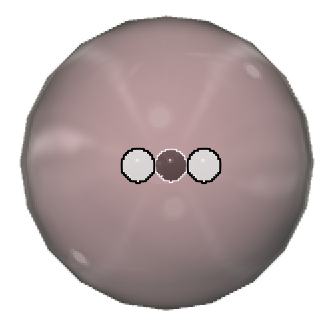tritium (1H3).
Some isotopes are stable but others are radioactive. By way of example, uranium has two primary isotopes, the more stable 92U238 and the radioactive 92U235. Over 99% of uranium atoms have a mass of 238 atomic mass units, and only less than 1% have a mass of 235 amu. This is the reason uranium atoms must be separated in a centrifuge in order to collect enough 92U235 for use in a reactor or a bomb.
L
Linear Spin Bonding (LSB):
When two unpaired, degenerate electrons share an atomic shell and are able to align linearly and parallel to each other (as is proposed to be the case in the 3rd shell of pd-hybridized titanium, Ti), the parallel magnetic alignment of their spins allows for the reduction of energy through field cancellation. This is here proposed to be a possible explanation for titanium having a much lower magnetic susceptibility (χm) value with two unpaired core electrons than scandium (Sc) has with only one.
There are other forms of spin bonding, such as parallel spin bonding, total di-electron inclusion, partial di-electron inclusion, ferromagnetic spin bonding, as well as that responsible for the formation of the di-electron.
References: A. Benn, J.G. Williamson, ‘The Photonic Topology Of Quantum Spin’, Quicycle Journal, 2022. Arnie Benn: The Physics Of Sub-Quantum Spin, followed by this Q&A.
London Dispersion Force:
When two (neutral) atoms or molecules approach each other, their electron clouds experience mutual repulsion. This causes the electrons on both of them to shift slightly so that a weak polarity is induced. If there are enough electrons present (because the atoms are larger), this polarity can become quite meaningful. If temperatures are low enough to minimize particle movement, this temporary polarity can be enough to stick particles together to form a solid. Example: iodine (I2) molecules at room temperature form a solid, though not bromine (Br2) molecules, which form a liquid, or chlorine (Cl2) molecules, which form a gas. This is because, the fewer electrons they have, the weaker the dispersion forces between them. Liquids feature particles with weaker forces holding them together, while gases have little to no appreciable cohesion between particles.
M
M.A.R.T.:
The “Mathematics of Absolute Relativity Theory.”
MART is an evolving Clifford-Dirac algebra designed to encapsulate Absolute Relativity — the fully relativistic sub-quantum mechanics approach required in the context of the rotating photon model of matter. The mathematics is designed to be highly and appropriately constrained in order to represent what nature does and to exclude what nature does not do. (See Williamson Equation below.)
Its purpose is also to develop into a solution of Hilbert’s 6th. It is named in memory and honor of founding Quicyclist, Dr. Martin van der Mark. (It was originally dubbed ‘the Mathematics of Absolute Relativity Theory In Nature’ — M.A.R.T.I.N. — but we have just come to call it MART.)
Software tools are in development in order to facilitate the use of MART in modeling and engineering. (See: Computational Tools.)
One of the great utilities of MART is the ability to work with each element of a system’s energy flow in its correct and fully relativistic ‘space.’ (See momentum space.)
References: J.G. Williamson, A. Benn, M. Rudolph, ‘Quantum Spin Coherence In 4 Derived 3-Spaces’, Quicycle Journal (2022) J.G. Williamson, ‘A New Linear Theory Of Light And Matter’, J. Phys. (2019) J.G. Williamson, Absolute Relativity Theory: A Proposed Solution To Hilbert’s 6th.
Magnetic field space:
When dealing with magnetic field, in the mathematics of absolute relativity theory (MART), it is dealt with differently from electric field or spin, for example. Magnetic field is a bi-vector quantity, a differential involving 2 dimensions of space (but no time dimension). (see spacetime.) Magnetic field is a directed 2-dimensional space-space plane element (Ξjk) in M.A.R.T.
It is useful to refer to this mathematical construct as magnetic field space, even though it is nothing more than a subset of normal 4-dimensional spacetime. (See momentum space for more detail.)
Reference: J.G. Williamson, A. Benn, M. Mercury, ‘Quantum Spin In 4 Derived 3-Spaces’, Quicycle Journal, 2022.
Magnetic Permeability (μ0):
See spacetime.
Magnetic Susceptibility (χm):
This is a measure of the extent to which a substance ‘becomes magnetized’ when exposed to an external magnetic field, and thus, resonates together with the field. It is therefore also a measure of how strongly an element will be attracted (or repelled) by an external magnetic field.
A negative value means the element is diamagnetic — it has all of its electrons paired and it repels from an external magnetic field. A positive value means the element is paramagnetic — it has unpaired electrons and it is attracted into an external magnetic field.
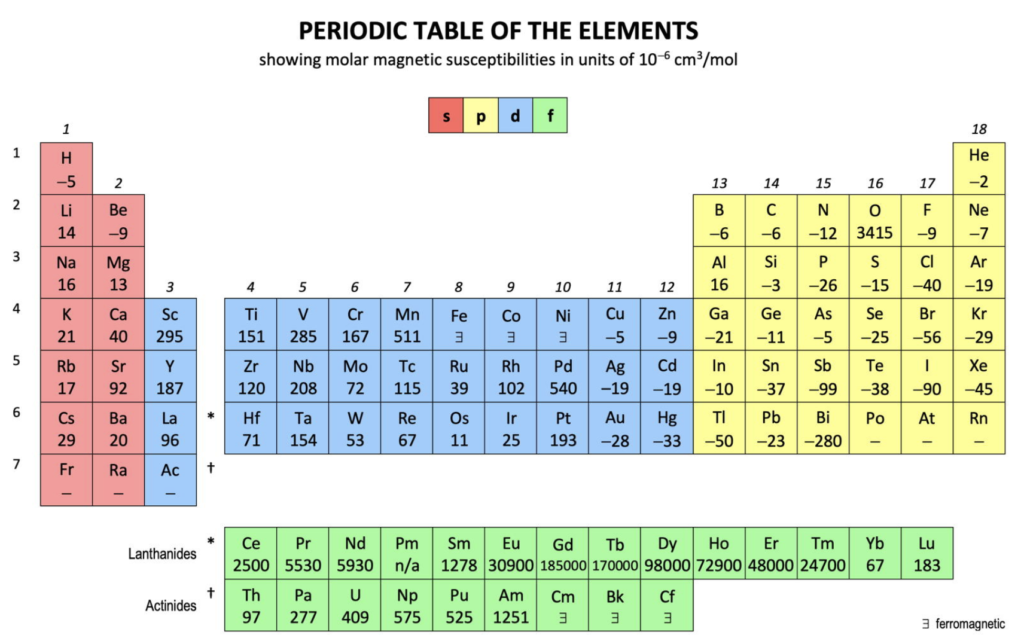
(See paramagnetic strength trend analysis for more detail.)
Magnetism:
Magnetism can be understood as a force of attraction or repulsion resulting from the flow of electric current or the spin of a charged particle. According to both the Williamson-van der Mark and Robinson models, subatomic particles are made of self-confined knots of electromagnetic radiation, and as such, they cause electric and magnetic fields to be introduced into the spacetime around them.
In the toroidal, double-loop rotation of the electron, for example, chirality is immediately a characteristic of the system, and this naturally divides ‘spin reactions’ (magnetism) into two complementary forms that we call north and south. They are simply the two relative chiral orientations of the rotating electromagnetic flow. By way of example, Earth’s rotation will appear right-handed (counter-clockwise) when viewed from above the north pole, but left-handed (clockwise) when viewed from above the south pole.
In an electron, the (instantaneous) north magnetic pole lies along the axis running through the center of the toroidal topology, in the direction of the thumb in a left-handed chiral rotation. South lies in the opposite direction along the same axis. In an isolated electron, the magnetic field averages to zero (due to the electron’s spherically-symmetrical spin). The magnetic moment of the electron emerges only in the presence of an external field, which breaks the internal spherical symmetry of an isolated electron.
When the influence of a particle’s magnetic spin is extends into the spacetime around it, other magnetic fields respond to it when they encounter it. The magnetic fields of other nearby electrons will therefore interact with this electron’s field in such a way that north repels north but attracts south. This ultimately derives from the fact that angular momenta are either working together, ‘counter-rotating’ in balance and lowering energy (attraction), or ‘co-rotating’ in such a way that increases energy (repulsion).
An unpaired electron therefore has a magnetic field as a result of its spin and its internal toroidal photon topology. (Similarly, its electric charge arises from the topology of its electric field.) When many (unpaired) electrons exist in concert, for instance within a solid crystal, various different forms of magnetism can result, depending upon their geometry and interactions. Some of these will be discussed below.
The most well-known form is ferromagnetism, in which the unpaired electrons throughout a metal crystal align their magnetic spins, and are able to hold this crystal-wide alignment. The crystal as a whole then manifests a macro-magnetic field, becoming a permanent ‘ferromagnet.’ The most important example of this occurs in iron (Fe).
When electrons (with opposite spins) pair up, on the other hand, they superimpose in a way that finds them perfectly anti-parallel. This allows their magnetic fields to cancel against one another, which lowers energy significantly, making this a highly favorable state. One example of this is the electron shell of a helium (He) atom. Due to its internal magnetic field cancellation, this di-electron pair is no longer attracted towards other magnetic fields, but rather, repels them. This is called diamagnetism, and it happens in order to maintain the pair’s lowest energy state of perfect field cancellation.
For more detail, see Magnetism & Magnetic Trends.
Mass:
Radiant (electromagnetic) energy and matter are two forms of the same root-energy ‘stuff.’ According to (the sub-quantum mechanics of) the Williamson-van der Mark and the Robinson Models, particles that have mass, such as electrons, are really photons of light that are traveling in a circle (or knot) rather than in a straight line. Such concentrated, self-sustaining photon resonance structures are the essence of matter. They confer mass on particles by virtue of the way that rotating photons interact with the fabric of spacetime to generate gravity. The more matter is present, the greater the gravitational effect, and thus, the larger the mass.
This conception of mass, as arising from the dynamic energy flow within a particle, extends beyond that represented in the Dirac equation, where mass is inserted as a separate, static (scalar) quantity. This is simply because, prior to the development of sub-quantum mechanics, this dynamics was unknown and inaccessible.
By virtue of having energy (E), an object has mass (m), according to the equation E=mc2. Since photons have energy, they also have mass — inertial mass. They do not possess rest mass, but that is because they do not exist at rest! Photons are known to have momentum, however, and that is not possible without inertial mass.
References: J.G. Williamson, M.B. van der Mark, ‘Is The Electron A Photon With Toroidal Topology?’, Annales de la Fondation Louis de Broglie (1997) J.G. Williamson, ‘A New Linear Theory Of Light And Matter’, J. Phys. (2019) Physical Explanation of Einstein’s Gravity, J. Phys. Commun. 2021 Vivian Robinson: Visualizing Sub-Quantum Gravity followed by this Q&A.
Metal:
On the periodic table, elements on the left side are considered metals and elements on the right side are considered non-metals. The dividing line between them is a diagonal ‘staircase’ of elements that are considered semi-metals or metalloids. These include B, Si, Ge, As, Sb, Te & At. Elements become more metallic in character the further they get from the metalloids towards the left bottom corner of the table. The reason for this is that larger atoms will give their outer electrons more easily because they are further from the nucleus and therefore less strongly bound to it. (See Periodic Trends for more detail.)
Metal atoms bond to one another via metallic bonds. A metal can be a pure element, such as a bar of gold, or an alloy of different metals, such as bronze, which is a mixture of copper (Cu) and tin (Sn).
Metallic bond:
Metallic bonds occur between metal atoms (ex: bronze, Cu+Sn, or pure silver, Ag). Metals occupy the left-side columns of the periodic table, and they represent atoms with low electronegativity that are willing to relinquish one or more outer electrons in order to reach the stability of a full electron shell.
When many metal atoms occur together, as a solid crystal, they are able to share their outer-shell electrons, which become delocalized into a background matrix of electron density known as a 3D ‘electron gas’ in solid state physics. It is within this matrix of electron density that the now-positive and full-shell atomic cores remain suspended. They are held in place by their mutual repulsion, as well as their attraction to the electron gas in which they are suspended.
As a result of their delocalized electrons, most metals are good conductors of electric current.
Metalloid:
On the periodic table, the elements B, Si, Ge, As, Sb, Te & At are considered semi-metals or metalloids because they lie between the metals and non-metals on the periodic table. This gives them unique properties as a result.
Molecule:
A combination of two of more atoms bonded together. Simple examples include the hydrogen molecule (H2), the oxygen molecule (O2), and the water molecule (H2O). More complex examples include protein and DNA molecules, which can contain hundreds or even thousands of atoms.
Momentum space:
Momentum space (or spatial frequency space) is a mathematically derived ‘space’ in which we can represent a momentum.
Mathematically derived spaces arise when we multiply or divide vectors or ‘spaces.’ Such operations can, for example, convert vector quantities to bi-vector, tri-vector, or quadri-vector quantities, or vice versa.
By way of example, velocity is a bi-vector quantity since it is ‘derived’ by taking a time derivative of a distance (dx/dt). When we divide a space vector by a time vector, we get a velocity bi-vector. We are then in a bi-vector space. Since vectors and bi-vectors transform differently in a fully relativistic mathematics, they must each be dealt with in their appropriate ‘space.’
These ‘derivative spaces’ can be very useful for working with different aspects or elements of energy flow in spacetime. This is because electric field (a space-time bi-vector), magnetic field (a space-space bi-vector), and spin (a space-space-time tri-vector), each live in a different, linearly independent space. (See Quantum Spin Coherence In Four Derived 3-Spaces for more detail.)
Momentum is a product of two other properties — mass and velocity. In the diagram of the electron below, the Poynting vector — an angular momentum around the torus — is depicted by the red arrows that trace the torus. It represents a cross product between an electric field vector (the green spines) and a magnetizing field (the blue spines). As such, the diagram of the Poynting vector path for the electron depicts momentum space rather than normal 3-dimensional ‘space-space.’ This momentum is also defined at a point. It is therefore helpful to see it less like ‘a roller-coaster moving around a stationary track’ than like ‘a track moving through a stationary roller-coaster.’ A diagram of a momentum should therefore not be taken too literally.
In the case of the composite diagram of the electron (above), the sphere in the center shows how this momentum path transforms into normal 3-D space. In electric field space, a free electron’s charge will be spherically symmetrical. (Since the electron is a light-speed particle on the ‘inside,’ its geometry will project, in a fully relativistic way, into whichever reference ‘space’ we project it.)
Note carefully that these referenced 3-spaces — momentum space, electric field space, magnetic field space, or spin space — are simply different divisions (or differentials) of 4-dimensional spacetime, yielding different 3-dimensional subsets of spacetime. This separation into ‘spaces’ is therefore only a mathematical convenience in order to deal more accurately with each aspect of a particle’s energy flow.
There is, in reality, only one spacetime, made up of three dimensions of space and one of time — x, y, z, and t. The mathematical inverses of space and time, and their products, quotients and differentials, lie in sets of linearly independent spaces. (See M.A.R.T.) These prove to be of physical significance because they allow charge, field, and spin to be evaluated both separately or together, and in a fully relativistic context.
Reference: J.G. Williamson, A. Benn, M. Mercury, ‘Quantum Spin Coherence In 4 Derived 3-Spaces’, Quicycle Journal, 2022.
N
Neel Temperature (TN):
The temperature at which the electrons in an antiferromagnetic metal lose their alternating spin alignments and they become paramagnetic. This means they will be able to align in the same direction as an external magnetic field. It occurs because there is enough thermal energy at this temperature that the spin orientations between unpaired electrons on adjacent atoms can be disrupted.
Network covalent bond:
Network covalent bonds occur between non-metal atoms that form solid crystals (ex: C in diamond). Non-metals occupy the right-side columns of the periodic table, and they represent atoms with high electronegativity that strongly attract electrons because they want to complete their almost-filled electron shell. When many non-metal atoms occur together in a crystal, none will be willing to relinquish an electron. They are therefore forced to share electrons. That way, none of the atoms feel like they have lost an electron but all feel like they have gained one (or more). With multi-directional covalent bonds being formed by each atom with those around it, network covalent bonds form extremely stable and strong structures, resulting in some of the hardest materials on the planet. Diamond is an example, a crystal made of a network of carbon atoms bonded in a perfect tetrahedral crystal lattice.
Neutron (n0):
The neutron is one of the three subatomic particles that make up all atoms. (The other two are the proton and the electron.) Neutrons carry no overall charge and are found in the central nucleus of the atom along with the protons. Protons and neutrons each have more than 1,800 times more mass than an electron.
According to the standard model of physics, the neutron is believed to be a composite particle made up of three quarks — two ‘down’ quarks and one ‘up’ quark — that are held together by a binding energy. The quarks constitute about 1% of the neutron’s mass-energy and the binding energy contributes the remaining 99%.
According to The Robinson Model of Nuclear Binding, like all subatomic particles, the neutron is made of a photon of light of the appropriate energy making two revolutions per wavelength. While a charged particle like the proton will be made of a circularly-polarized photon, a neutral particle like the neutron will be made of a plane-polarized photon. The neutron’s lack of charge arises from the plane-polarization of its inner photon. The orientation of its electric field, as it makes its double loop rotation, is such that the positive and negative fields alternate pointing outwards. While each resonant element within the neutron’s structure has charge, the overall result is a net neutral particle. As a result of its plane-polarization, an isolated neutron is not stable. It usually decays within 15 minutes, splitting into a proton, an electron, and an anti-neutrino. (The latter is the means by which the angular momentum of all the particles involved in the transition is conserved.) When bound to a proton within a nucleus, however, a neutron is stable as a result of the resonance and field sharing between the particles.
While in the case of the electron, the internal photon traces a toroidal path in (momentum) space as it completes its double-loop rotation, in the case of the neutron, it is a little more complex. Since the neutron contains more than 1,800 times the mass-energy of the electron, according to the Robinson Model its rotating photon resonance also contains higher energy harmonics of its fundamental rotation — 1/3rd, 1/9th, and 1/27th harmonics. These charged harmonics resonate in the equatorial plane while the (toroidal) magnetic field loops around in the axial direction.
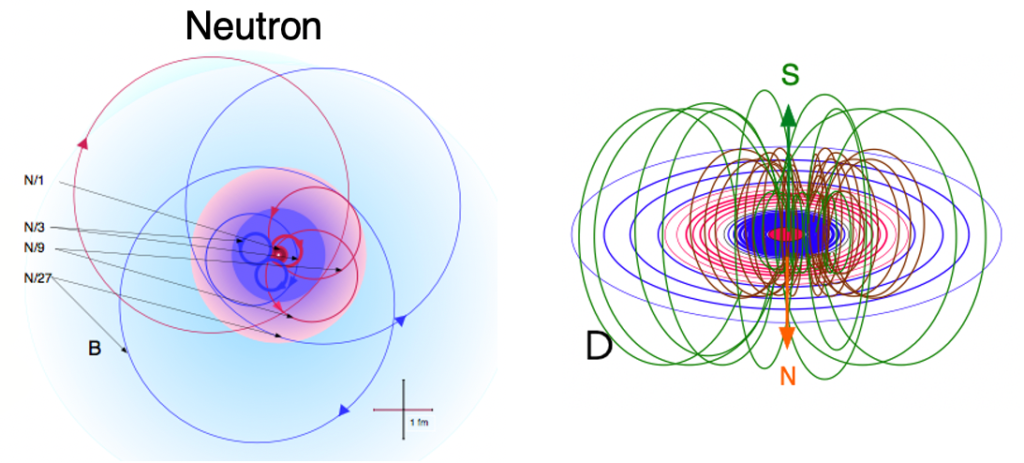
Since quarks have never been isolated and seem to occur only in their groupings of three, the photon harmonics of the Robinson Model may provide insight into why quarks do not occur except as part of such a stable resonance.
In atoms, neutrons are very important, not simply because they separate the positive protons — whose like charges repel — but because they actually bind the protons together electrostatically. The exterior 1/27th photon harmonic of the neutron is negative, and binds to the positive exterior resonance of the proton through an overlapping ‘division-by-zero’ attraction. As a result of being made of a rotating photon, a neutron has a quantum spin of S=½ℏ. The mass of the neutron (939.6 MeV) is very similar to (though slightly larger than) the combined masses of the proton (938.3 MeV) and electron (0.511 MeV). The difference in their masses represents the difference in energy between the neutron state and the electro-proton state that is the hydrogen (H) atom.
References:
Vivian Robinson: The Common Sense Universe Vivian Robinson: The Structure Of Electrons, Protons, Neutrons & Neutrinos Vivian Robinson: The Robinson Model Of Nuclear Binding For more videos in this Robinson series, click here.
Neutrino:
The neutrino is the smallest stable subatomic particle. It has no charge, no magnetic moment, a spin of S=½ℏ, and an exceedingly small mass-energy content of the order of 10-4 eV. That energy corresponds to the peak energy of the cosmic microwave background radiation temperature of ~2.7°K. Cosmological neutrinos constitute by far the most common component of the universe with a density of about 1012 neutrinos per cubic meter (see more here). Like the electron, it is comprised of a single photon of the appropriate energy making two revolutions per wavelength. Neutrinos can travel at very high speeds approaching the speed of light. While they do not easily interact with matter, neutrinos can be either captured or released during the process of one subatomic particle morphing into another. When a neutron decays into a proton and an electron, for example, a neutrino is also produced as a by-product of the reaction, and it will have a spin opposite to that of the electron. This is the means by which the angular momentum (spin) of all the particles involved in the transition is conserved. In addition, the universe is literally completely filled with neutrinos. Like electrons, neutrinos are not point particles. They are rotating photon loops, just like all other particles, and they have size. There are over a million cosmic neutrinos in every cubic millimeter of space, and each one has a radius of about 2 millimeters. That provides a continuous effect through all of space, a ‘substrate’ with the same quantum spin as the electron, through which all photons must travel.
References: Vivian Robinson: The Common Sense Universe Vivian Robinson: The Structure Of Electrons, Protons, Neutrons & Neutrinos For more videos in this Robinson series, click here.
Non-metal:
On the periodic table, elements on the left side are considered metals and elements on the right side are considered non-metals. The dividing line between them is a diagonal ‘staircase’ of elements that are considered semi-metals or metalloids. These include B, Si, Ge, As, Sb, Te & At. Elements become more non-metallic towards the top right corner of the table. The reason for this is that smaller atoms with almost-full electron shells will attract electrons the most strongly. The right-most column, the Noble gases, are generally unreactive because they are both neutral and have full electron shells. (See Periodic Trends for more detail.) Covalent bonds occur between non-metal atoms (ex: H2O).
O
Orbital:
A region of space around a nucleus (or around the nuclei of a molecule) that is occupied by (high) electron density. There are four types of orbitals: s-, p-, d-, and f-orbitals. These vary in size and shape, with the simplest being the s-orbital — a sphere of electron density that envelops the nucleus in a spherical stationary wave of electron density. (The four main blocks into which the periodic table is divided correspond to the s-, p-, d-, and f-orbitals.)
When two or more electrons are held (electrostatically) within the charge well of the same nucleus, they will naturally optimize their arrangement into orbital regions that lower energy by minimizing mutual electron repulsion. Electrons will also re-arrange their configurations when local electronic conditions change. (See hybridization.)
Even though it is often useful to talk about these orbitals as separate, they are — the entire atoms is — all part of a single, coherent, harmonic, resonant, phase-locked, spherically-symmetrical quantum wave state, and it is all electromagnetic at the root-energy level. Orbitals and their ‘boundaries’ can be seen as nothing more than nodes and antinodes in this harmonic wave structure.
References: A. Benn, J.G. Williamson, ‘pd-Hybridization And The Electron Geometry Of Fluorine, Neon And Iron’, Quicycle Journal, 2024.
P
Parallel Spin Bonding (PSB):
When unpaired, degenerate electrons share an atomic shell, their lowest energy state is achieved when they possess the same sub-quantum spin and when they are in a parallel magnetic alignment. This is known as Hund’s Second Rule, and PSB is here proposed as an explanation of the physical mechanism underlying this phenomenon.
There are other forms of spin bonding between electrons, such as linear spin bonding, partial di-electron inclusion, ferromagnetic spin bonding, as well as that responsible for the formation of the di-electron — total di-electron inclusion.
References: A. Benn, J.G. Williamson, ‘The Photonic Topology Of Quantum Spin’, Quicycle Journal, 2022. Arnie Benn: The Physics Of Sub-Quantum Spin, followed by this Q&A.
Paramagnetism:
This is when a substance is attracted to a magnetic field because it contains one or more unpaired electrons. In the presence of an external magnetic field, the magnetic field of an unpaired electron will cause it to align with the magnetic field. This causes cancellation of magnetic field to occur between the electron and the direction of the field, which lowers energy. The substance will therefore experience an attraction into the magnetic field. Many molecules, such as dioxygen (O2), and most metals are paramagnetic.
The strength of an element’s paramagnetism (see magnetic susceptibility) has to do with the number of unpaired core electrons, with their effects reduced as a result of the internal field cancellation and spin-bonding occurring within the atom’s pd-hybridized electron geometry.
The following diagram shows the relative paramagnetic strengths of the transition metals. (See paramagnetic strength trend analysis for more detail.)
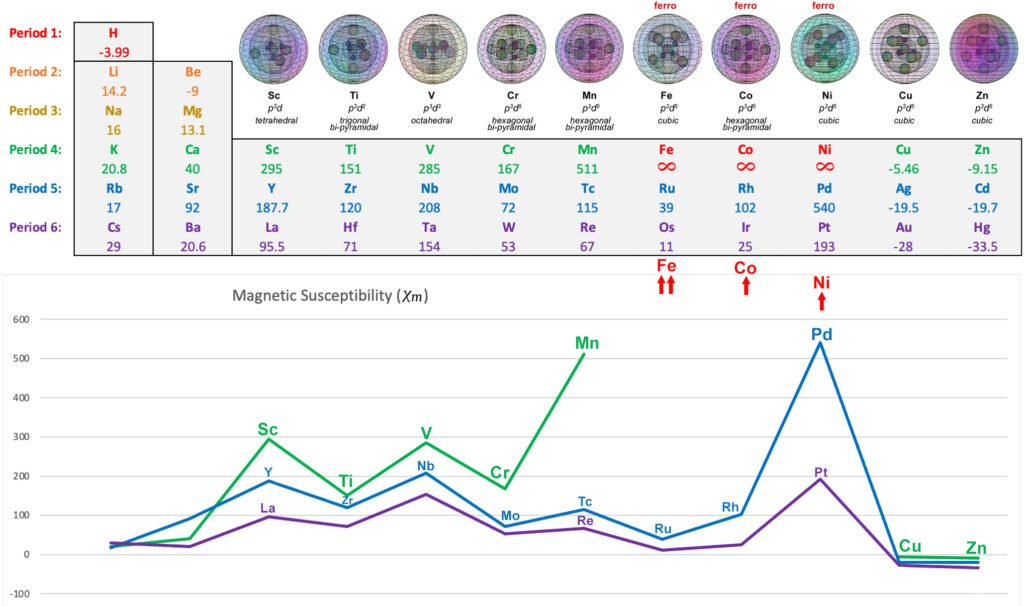
( CLICK HERE to watch a clip explaining the physical mechanism behind paramagnetism, on the Demystify Sci podcast.)
Partial di-electron inclusion (PDI):
It is proposed that a form of spin bonding called partial di-electron inclusion (PDI) can also occur between unpaired electrons of opposite spin on adjacent atoms in a molecule, if they are close enough to interact. It is suggested that this coherence can stabilize otherwise unpaired electrons into a symmetrical quantum state without requiring them to pair up completely. This finds application in orbitals such as the resonance state of the ozone (O3) molecule.
There are other forms of spin bonding between electrons, such as linear spin bonding, parallel spin bonding, ferromagnetic spin bonding, as well as that responsible for the formation of the di-electron — total di-electron inclusion.
References: A. Benn, J.G. Williamson, ‘The Photonic Topology Of Quantum Spin’, Quicycle Journal, 2022. Arnie Benn: The Physics Of Sub-Quantum Spin, followed by this Q&A.
*
Pauli’s Exclusion Principle:
Pauli’s Exclusion Principle states that two electrons with the same spin cannot occupy the same quantum state. This means that two spin-up electrons cannot occupy the same orbital, and they will not be able to bond with one another. A spin-up and a spin-down electron will be able to occupy the same orbital and they will eagerly superimpose into a bonding (di-electron) relationship.
This quantum mechanical ‘rule’ was derived from observation, but according to the traditional understanding (see here), no physical explanation was offered as to why it had to be this way.
A possible explanation of this spin-mediated physical mechanism is proposed by Williamson and Benn.
References: J.G. Williamson, A. Benn, M. Mercury, ‘Quantum Spin In 4 Derived 3-Spaces’, Quicycle Journal, 2022. A. Benn, J.G. Williamson, ‘The Photonic Topology Of Sub-Quantum Spin’, Quicycle Journal, 2022. Arnie Benn: The Physics Of Sub-Quantum Spin, followed by this Q&A.
pd-Hybridization:
This is a proposed concept of hybridization (see reference) in which only the p– and d–orbitals need to hybridize together in order to achieve up to 8-directional symmetry. The s-orbital is not needed for symmetry, as it is in the case of sp3-hybridization. The s-orbital electrons can therefore remain in their di-electron state, as a form of fundamental resonance, upon which (or within which) the hybrid orbitals resonate like harmonics upon a fundamental.
References: A. Benn, J.G. Williamson, ‘pd-Hybridization And The Electron Geometry Of Fluorine, Neon And Iron’, Quicycle Journal, 2024.
Periodic Table:
A chart containing all of the elements that have been discovered. They are arranged in order of their number of protons (atomic number), as well as in rows and columns. These reflect the periodic nature of their properties — that those in the same column exhibit similar properties, and those in the same row exhibit similar trends in their properties. This structure was first discovered by Russian chemistry professor, Dmitri Mendele’ev, in 1869.
Click HERE to visit the Quicycle Interactive Periodic Table of Atomic Orbitals, designed to investigate electron orbital geometry.
On the periodic table: most of the elements (on the left side) are considered metals and elements towards the top right are considered non-metals. The dividing line between them is a diagonal ‘staircase’ of elements that are considered semi-metals or metalloids. These include B, Si, Ge, As, Sb, Te & At (as shown in brown below).
Elements become more metallic in character the further they get from the metalloids, towards the left bottom corner of the table, and they become more non-metallic towards the top right corner of the table. The reason for this is that larger atoms and those with fewer outer electrons will give their valence electrons away more easily (which contributes to bonding and electrical conductivity in metals, for example), and smaller atoms with almost-full electron shells will attract electrons the most strongly (which is why many elements can be oxidized by oxygen).
The trends in properties that change across and down the periodic table include atomic radius, effective nuclear charge, electronegativity, and others. (See Periodic Trends for more detail.)
The right-most column — the Noble gases — are unreactive because they are both neutral and have full electron shells. (Exceptions occur when highly electronegative atoms like oxygen or fluorine approach the very large noble gas atoms such as krypton (Kr) or xenon (Xe). Molecules like XeF6 are therefore possible.)
Reference: Arnie Benn: Atoms & The Periodic Table: An Interactive Introduction
Pivot:
The scalar unit element (ΞP) in M.A.R.T. It has the same physical dimension as the magnetic field but transforms as a rest-mass rather than a field. (See Williamson equation for more detail.)
Photon:
A quantum (or ‘packet’ or bullet) of light energy. Electromagnetic radiation travels in discreet packets called photons. It does not travel in a continuous stream, as we might imagine when we look at a beam of light or a laser. There are usually so many photons being released so rapidly by a light source that it only gives the impression of being a continuous beam. In a typical circularly-polarized photon, the electric and magnetic fields spiral around the axis of travel, 90 degrees apart. The fields complete one revolution around the axis for every wavelength. This gives the photon a quantum spin = ℏ, making it a boson. The spin of a photon can also be excited up to higher spin states, but they can only be integer spin states (nℏ), for instance S = 2, 3, 4, etc.
While photons have no rest-mass — since they do not exist at rest — they do have inertial mass, by virtue of their internal energy. (See E=mc2.)
Planck’s constant (h):
The concepts of energy (E) and frequency (𝜈) can, in some senses, be thought of as representative of one another. The energy of a quantum system can be represented by its frequency because energy and frequency are related via the equation E=h𝜈.
Since energy is measured in units like joules (J), and frequency is measured in units like Hertz (s-1), in order to convert energy units into frequency units, or vice versa, we need a conversion ratio. Planck’s constant is that ratio, and its numerical value is equal to 6.626 x 10-34 J.s.
Planck’s constant (h) is named in honor of the scientist who discovered this relationship, Max Planck.
Since so much of quantum energy flow exists within a rotational frame — photon spin and rotating-photon particle structure (see quantization) — it is important to have a rotational equivalent for Planck’s constant. As such, when we divide Planck’s constant by the circumference of the unit circle (2π) we get h/2π, the reduced Planck’s constant, commonly known as h-bar (ℏ). The rotational equivalent of the above equation would therefore be E=ℏω (where ω represents angular velocity).
Polar:
If an atom or molecule has asymmetry in its electron cloud so that one side has more electron density than the other, it will feel partially positive on one end and partially negative on the other end. This separation of charges is called polarity, and it gives such atoms or molecules forces of attraction and repulsion that are meaningful, though not quite as strong as full ionic charges. Polar molecules are therefore attracted to one another. If the electron cloud is symmetrical or identical on opposite sides of the atom or molecule, then it will be non-polar. (Non-polar molecules are only slightly attracted to one another as a result of London dispersion forces.)
If atoms in a molecule share the electrons is a bond equally (because they are the same atom), then such bonds will be non-polar and therefore purely covalent in nature. If the electrons in a bond are shared unequally (by different atoms), the bond will be polar. The more unequally shared, the more polar the bond. If the sharing becomes so unequal that one atoms ends up stealing the electron completely from the other, ions will result, and an ionic bond will form as a result of the strong electrostatic attraction between the (full) charges.
Positron (e+):
A positively charged subatomic particle, identical to the electron, except that it has the opposite charge. It is the electron’s ‘anti-particle,’ and this illustrates the concept of antimatter. It is ‘anti’ in the sense of its charge being opposite, and it also has opposite spin. Like the electron, it is made of a single photon of light making two revolutions per wavelength. A positron is thus a self-confined knot of concentrated light energy traveling around itself at the speed of light, and it therefore has a toroidal (donut-shaped) sub-structure in (momentum) space. As a result of the geometry of this double-loop torus, the photon’s positive electric field is pointing outwards at all times, which is what gives the positron its positive charge. When an electron and a positron meet, they unlock each other’s photons’ angular momenta, converting their rotating photons to linear photons in an explosion of pure energy called a matter-antimatter annihilation. A positron has a right-handed spin of S=½ℏ, a charge of C=+1.6×10-19 Coulombs, and a mass-energy content of 511 keV.
Proton (p+):
The proton is one of the three subatomic particles that make up all atoms. (The other two are the neutron and the electron.) Protons are stable, carry a positive charge, and are found in the central nucleus of the atom along with the neutrons. Protons and neutrons each have more than 1,800 times the mass of an electron.
According to the standard model of physics, the proton is believed to be a composite particle made up of three quarks — two ‘up’ quarks and one ‘down’ quark — that are held together by a binding energy. The quarks constitute about 1% of the proton’s mass-energy and the binding energy contributes the remaining 99%.
According to The Robinson Model of Nuclear Binding, like all subatomic particles, the proton is made of a photon of light of the appropriate energy making two revolutions per wavelength. While in the case of the electron, the internal photon traces a toroidal path in (momentum) space as it completes its double-loop rotation, in the case of the proton, it is a little more complex. Since the proton contains about 1,836 times more mass-energy than the electron, its rotating photon resonance also contains higher energy harmonics of its fundamental rotation — 1/3rd and 1/9th harmonics. These charged harmonics resonate in the equatorial plane while the (toroidal) magnetic field loops around in the axial direction.
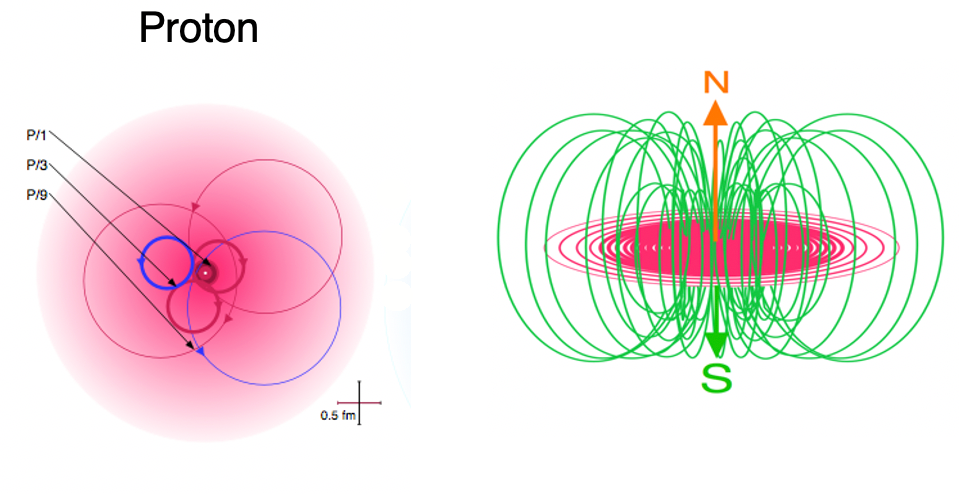
Since quarks have never been isolated and seem to occur only in their groupings of three, the photon harmonics of the Robinson Model may provide insight into why quarks do not occur except as part of such a stable resonance.
Protons are important because atoms of a given element are identified according to their number of protons. This is called the atomic number, and the periodic table of the elements is laid out in order of atomic number. The first element on the periodic table, hydrogen, has 1 proton. The second element, helium, has 2 protons, and so on. It is also the presence of the protons in the central nucleus that attracts electrons to the atom, specifically in order to neutralize their charge. Neutrons are attracted into the mix not only in order to separate the protons from one another (since their like positive charges repel one another) but to bind the protons together (since, according to the Robinson Model of Nuclear Binding, the exterior resonance of the neutron is negative).
As a result of being made of a rotating double-loop photon, a proton is a fermion and has a quantum spin of S=½ℏ. It has a mass-energy content of 938.3 MeV and carries a charge of +1.6×10-19 Coulombs. According to the Robinson Model, the proton’s charge arises from the fact that the orientation of its internal circularly-polarized photon’s electric field, as it makes its double-loop rotation, is such that the positive field polarity is outwardly directed for the majority of its harmonic oscillations, and in particular, for the inner- and outermost ones. This results in a net positive charge for the particle.
References: Vivian Robinson: The Common Sense Universe Vivian Robinson: The Structure Of Electrons, Protons, Neutrons & Neutrinos Vivian Robinson: The Robinson Model Of Nuclear Binding For more videos in this Robinson series, click here.
Q
Quantization:
Quantization is not merely a set of axioms. It is a consequence of underlying physical processes, emerging from the fact that energy and matter possess an intrinsic wave nature. Waves necessarily contain boundary conditions. Quantum spin, like all stable harmonic wave resonances, must be quantized. Put simply, a rotation through 2π (or 4π for fermions) must bring one back to the starting point, which must constitute an integer number of wavelengths. This is the reason that quantum spins either have a value in integer units of ℏ or ½ℏ.
“This is the proper origin of quantization in quantum mechanics.” — John Williamson.
For any coherent system, each element of field, spin, and mass-energy flow must attain harmonic phase coherence, both with itself and with every other element. The total energy of a system may then be viewed either as an integration over the total field energy density, or as a quantum energy based on the frequency through E=h𝜈.
It is therefore the internal dynamics of particles (rotating photons) and their inter-actions (photons) that give rise to the most fundamental aspects of the quantization of charge and spin. (See Williamson equation.)
Related content: J.G. Williamson, A. Benn, M. Rudolph, ‘Quantum Spin Coherence In 4 Derived 3-Spaces’, Quicycle Journal, 2022. J.G. Williamson, ‘A New Linear Theory Of Light And Matter’, J. Phys. (2019)
Quantum:
‘Quantum’ means ‘countable.’ It means that something happens in integer units. It also implies that changes must occur in discrete steps rather than in a smooth, continuous gradient. These ‘quantum leaps’ of change mean that the process or system is quantized. Stairs and piano keyboards are examples of things that are quantized. Ramps and violins are not. The fundamental reason for quantization is that waves resonate in multiples of their wavelengths, rather than at arbitrary points in between. Subatomic particles are made of photons that make double-loop rotations. They are only stable if their rotations are in multiples of double-loops. A “quantum” of light is called a photon, and it is the amount of electromagnetic energy that is emitted, transmitted, or absorbed in a quantum inter-action. A photon can even have a very high energy, which means that each packet of energy at that wavelength carries a large amount of energy. An example is the gamma ray. Electron clouds in atoms can also only manifest certain discrete electron states. This is because each electron is an identical unit, and because their interactions result in discrete, resonant, stationary wave states. Electron clouds transition between adjacent energy states by emitting or absorbing whole photons (or electrons) — one quantum at a time.
Quantum Inversion (Q.I.):
An inverse is a mathematical reciprocal. Dividing by a number is the same as multiplying by the inverse of that number. As such, division, multiplication, differentiation, and inversion are intimately related.
Division is familiar for simple numbers: the inverse of three is one third. However, what, physically, is the inverse of space? Or time? Or space-time? Or space divided by time? Or space-time on the light-cone?
If one can find an inverse for a number, the product of this with its starting quantity leads to a unit Lorentz scalar. It may be suspected, as indeed turns out to be the case, that finding such combinations may lead, in turn, to unitary processes which leads in turn to “allowed” and interesting physics. The extension of the unit relativistic vectors of space and time leads to a rich set of combinations of derived elements, corresponding to combinations of physical areas, volumes, and point, as well as base lines, where division is undefined.
Inversion is the underlying process of photon emission and absorption. It is the transformation that is required in order for a photon to go from an emitted thing to an absorbed thing.
References: J.G. Williamson, ‘Inversion And General Invariance In Spacetime’, Quicycle Journal, 2016 M.B. van der Mark, J.G. Williamson, ‘Relativistic Inversion, Invariance And Inter-Action’, Symmetry, 2021 J.G. Williamson: ‘Quantum Coherence And Quantum Collapse’ J.G. Williamson: ‘Relativistic Quantum Mechanics’
Quantum mechanics:
The science that describes light, subatomic particles, and their quantum interactions. It is based upon the idea that all interactions are quantized. Particles and energy states can be described by equations called wave-functions, since they are resonant wave states that are made up of photons.
When quantum mechanics is extended to include the effects of Special Relativity, it is called relativistic quantum mechanics (RQM).
Recent work by Williamson, van der Mark, and Robinson has further extended relativistic quantum mechanics into the realm within subatomic particles, and has therefore been dubbed sub-quantum mechanics. (See M.A.R.T.)
Quedgehog:
The 4-dimensional analog of the “Hedgehog”. Obviously.
It is a directed space-space-space-time 4-volume element (Ξ0123) in M.A.R.T. The element can be outwardly-directed or inwardly-directed.
Quicycle:
(Pronounced like ‘bicycle,’ but with a ‘Qu.’)
A contraction of the words “Quantum Bicycle.” It represents the turning, twisting, and tumbling motion of an electron (or positron) in free (4D) spacetime.
It is also short for ‘The Quantum Bicycle Society,’ whose website you are currently perusing .
R
Radioactivity:
In the nucleus of an atom, protons, which carry a positive charge, will repel each other unless they are held together by bonding electrostatically to neutrons, whose outer regions carry negative charge (see The Robinson Model of Nuclear Binding). The balance between protons and neutrons in the nucleus is therefore very important.
If a nucleus has either too many or too few neutrons, it lacks stability, and it may therefore begin ejecting or transmuting some of its subatomic particles in order to reach a stable configuration. This is called radioactivity, and it involves the ejection (or sometimes the absorption) of one or more subatomic particles or a photon of electromagnetic radiation, or both, from the nucleus.
Alpha radiation occurs when two protons and two neutrons are ejected in a cluster with a 2+ charge, called an alpha particle. (It is identical to the nucleus of a helium atom.) Beta radiation occurs when a neutron in the nucleus morphs into a proton by ejecting an electron and a neutrino. In the case of gamma radiation, only a (gamma ray) photon will be emitted. A radioactive decay therefore usually results in the atom turning into a different element.
Almost all of the radioactive atoms on the periodic table are those with the highest atomic numbers (and largest nuclei). For an explanation of this, along with more detail about nucleus formation and decay, see Robinson: The Common Sense Universe.
Reactivity:
This is a measure of how readily an atom will give or take electrons in order to achieve greater stability and lowest energy. If it has a low ionization energy and wants to lose electrons, a high ionization energy and wants to gain electrons, or if it has a high electron affinity and thus a strong desire to gain electrons, it will react vigorously with other elements in order to make those electron exchanges.
Redshift (z):
This refers to the stretching of the wavelength of light radiation. It can be caused by the Doppler effect or by photon interactions with mass and gravity. The Doppler effect occurs when a light source is getting further away, either because we are moving away from it or it is moving away from us. This causes its wavelength to appear longer and its frequency to therefore appear lower. The longer wavelengths of visible light lie at the red end of the rainbow spectrum, hence the name.
Redshift also result from a photon interacting with (or moving away from) a gravitational field. Photons have inertial mass (even though they have no rest mass), and they are therefore affected by gravity. Such interactions will reduce their energy. A reduction in energy means a reduction in frequency, and since the speed of light is constant, and this results in a relativistic increase in wavelength. This redshift is observed in solar photons arriving at Earth.
According to the Robinson model, the redshift of cosmic photons across vast distances is a result of spacetime having a form of ‘viscosity,’ resulting from the extremely high density of cosmic neutrinos. The rest mass-energy of the background neutrino flux, 10-4 eV/c2, has a temperature equivalent of 2.7K. Robinson proposes that a ‘micro-momentum’ loss of 0.00715% per million light years accounts for what is observed. (See more here.)
Relativity:
According to Albert Einstein’s Special Theory of Relativity, published in 1905, the speed of light is always constant for every observer, no matter their environment or how fast (or in what direction) they are traveling relative to the light. The consequence of this is that other perceptions become distorted in order to maintain this absolute.
One example is that time flows at a different ‘pace’ for observers who are traveling at very different speeds, especially when one or both of these speeds are a significant percentage of the speed of light. That is why high-speed cosmic travelers over large distances will always return home to find they have aged less than those they left behind. Calculating these differences is called a relativistic correction (or time dilation). The closer one travels to the speed of light, the more exponentially one’s perception of time will differ from those who remain ‘stationary’ on a planet. Since particles are made of rotating photons of light energy, these relativistic corrections automatically apply to all matter particles — their ‘internal clock,’ length, and mass.
Einstein’s Special Relativity is perhaps most famous for giving us the equation, E=mc2.
Robinson Model:
The Robinson model is an approach to physics forwarded by Dr. Vivian N. E. Robinson, inventor of the Robinson Backscattered Detector for scanning electron microscopes. The Robinson model is based in the four dimensions of spacetime (x, y, z, and t), its properties of electric permittivity and magnetic permeability (see spacetime), and the rotating photon model of matter. It encompasses the properties of photons, the rotating photon structure of the electron and other subatomic particles, nuclear binding, radioactivity, the nature of gravity, redshift, the large scale cosmological structures of the universe, and more.
For more detail on two of the main aspects of this work, see:
1. The Robinson Model Of Nuclear Binding:
– based upon the (Robinson) substructures of the proton and neutron
2. The Robinson Model Of Sub-Quantum Gravity:
– the “redshift metric” and a full gravitational solution
References: Vivian Robinson: The Common Sense Universe (ETP Semra) Vivian Robinson, ‘Physical Explanation Of Einstein’s Gravity’, J. Phys. Commun., 2021 Vivian Robinson: Visualizing Sub-Quantum Gravity followed by this Q&A Vivian Robinson: The Robinson Model Of Nuclear Binding For more videos in the Robinson series, click here.
Root-energy:
Root-energy (as in ‘square-root’ energy) refers to quantities that need to be ‘squared’ in order to represent an energy density. These include field-level elements such as electric field, magnetic field, and the quantum mechanical wave function, ψ. (In quantum mechanics, energy density is proportional to ψ†ψ.)
All 16 elements of the 𝚵𝒢 term in the Williamson equation represent root energies, at the level of field.
S
Spacetime:
The fabric of space and time, whatever it actually is, has two basic properties that we consider: its electrical permittivity (ε0) and its magnetic permeability (μ0). The former describes the extent to which spacetime can hold (or allow the passage of) electric fields, and the latter, the same for magnetic fields. The two properties are intimately related to the speed of light (c) because light is electromagnetic and interacts with space both electrically and magnetically. It can only travel because of its electric and magnetic interactions with spacetime. The three properties are related according to the equation ε0μ0=1/c2.
The term spacetime also relates to the fact that space and time are part of the same ‘stuff’ and cannot be separated, something that may seem unintuitive since we tend to think of time and space as separate things. Spacetime is also distorted by the presence of mass, which gives rise to gravity. Relativity also describes how aspects of space and time appear to become distorted under certain conditions so that the speed of light should appear constant to every observer in every reference frame.
Mathematically, it is interesting to note that different forms of energy interact with spacetime in different ways. The three variables of space are x, y, z, and the one variable of time is t. Spacetime is therefore 4-dimensional: x, y, z, t (and their inverses). The underlying nature of electric field is that it is a (3-component) flow, a rate of change of space by time (dx/dt, dy/dt and dz/dt), like velocity. The underlying nature of the (three component) magnetic field is that it is a twist, a rate of change of space by perpendicular space (dx/dy, dy/dz and dz/dx). No t. It makes things go around in a circle. Angular momentum (spin) is the rate of change of momentum with respect to perpendicular space, taking the form of d/dx(dy/dt).
‘Spang’:
The process of a photon being reflected back out into space from Earth. (If we could hear at the speed of light, it may also be the sound it makes.)
Spin (S):
Many subatomic particles have spin because they are made of a confined photon of light traveling in a circle, a double-loop rotation, at the speed of light (see electron). This is angular momentum at the sub-quantum level.
In the case of a charged particle, such as the electron, the (circularly polarized) photon of light making up the particle has an intrinsic angular momentum of h-bar (ℏ) because as it travels it spirals through 360° per wavelength. According to the Williamson-van der Mark model (see more here), electrons contain a second level of angular momentum in that their topology forms a double-loop rotation. This has an angular momentum of ½ℏ since it completes 720° per wavelength. The particle contains a third level of angular momentum in that this toroidal topology will tumble in the third orthogonal direction in order to conserve angular momentum (depending on the presence of an external magnetic field), also completing 360° per wavelength for a spin of ℏ.
According to the Robinson model, only charged particles contain intrinsic photon spin because they are made of circularly polarized photons. Neutral particles are made of plane polarized photons, and their angular momentum therefore arises entirely from their photon’s double-loop rotation (see more here).
It has also been proposed (Benn/Williamson) that the difference between a spin-up electron and a spin-down electron lies in the direction of circular polarization of the particle’s internal rotating photon. A photon with right circular polarization will condense to form an electron of one spin, and a left circular polarization will condense to form an electron of the opposite spin.
It has also been proposed that the relative spin states of adjacent electrons can interact in ways that are of significance, in that they can yield either a more or a less favorable energy condition. This is dubbed spin bonding (see below), and it is such interactions that underpin electron pair (di-electron) formation (and covalent bonding), Pauli Exclusion, and the energy lowering state described in Hund’s 2nd Rule.
References: J.G. Williamson, A. Benn, M. Mercury, ‘Quantum Spin In 4 Derived 3-Spaces’, Quicycle Journal, 2022. A. Benn, J.G. Williamson, ‘The Photonic Topology Of Sub-Quantum Spin’, Quicycle Journal, 2022. Arnie Benn: The Physics Of Sub-Quantum Spin, followed by this Q&A.
Spin bonding:
Spin bonding refers to a wave coherence, involving electron spin interactions, which lowers energy via an optimization of overall (average) spin, and sometimes also magnetic field cancellation.
One example is the formation of the di-electron, in which it is proposed that electrons of opposite spins superimpose, forming an interwoven, counter-rotating photonic state that places the spin phases (and magnetic fields) into a perfect balance. This creates a powerful spin-mediated coherence, resulting in a highly favorable energy state, here named ‘total di-electron inclusion‘ (TDI).
Another example occurs when (degenerate) electrons of the same spin achieve a symmetrical, parallel spin state (of the kind described by Hund’s 2nd Rule.) See parallel spin bonding.
In terms of electron in larger atoms and in the solid or molecular state, three other forms of spin bonding are suggested: Linear spin bonding occurs between electrons that are able to align in a linear and parallel fashion. It is proposed that a form of spin bonding called partial di-electron inclusion (PDI) can also occur between unpaired electrons of opposite spin on adjacent atoms, if they are close enough to interact. Another example has been proposed in recent work (see reference) in order to help explain the case of ferromagnetism in iron (Fe), and it has been named ‘ferromagnetic spin bonding‘ (FSB).
References: A. Benn, J.G. Williamson, pd-Hybridization And The Electron Geometry Of Fluorine, Neon And Iron’, Quicycle Journal, 2024. J.G. Williamson, A. Benn, M. Mercury, ‘Quantum Spin In 4 Derived 3-Spaces’, Quicycle Journal, 2022. A. Benn, J.G. Williamson, ‘The Photonic Topology Of Sub-Quantum Spin’, Quicycle Journal, 2022. Arnie Benn: The Physics Of Sub-Quantum Spin, followed by this Q&A.
Spin-down electron:
The relative direction of circular polarization (left or right) of the electron‘s internal rotating photon determines whether it is a spin-up or spin-down particle. Whichever direction is considered ‘up,’ the other will be considered ‘down.’ This results in a simple and binary relative spin reality for electrons.
See Spin.
References: A. Benn, J.G. Williamson, ‘The Photonic Topology Of Sub-Quantum Spin’, Quicycle Journal, 2022. Arnie Benn: The Physics Of Sub-Quantum Spin, followed by this Q&A.
Spin space:
When dealing with sub-quantum spin, in the mathematics of absolute relativity theory (M.A.R.T.), spin is dealt with differently from electric field or magnetic field, for example. Spin is a tri-vector quantity, a differential involving 2 dimensions of space and 1 dimension of time. (see spacetime above.) Spin is a directed 3-dimensional space-space-time element (Ξ0ij) in M.A.R.T.
It is useful to refer to this mathematical construct as spin space, even though it is nothing more than a subset of normal 4-dimensional spacetime. (See momentum space for more detail.)
References: J.G. Williamson, A. Benn, M. Mercury, ‘Quantum Spin In 4 Derived 3-Spaces’, Quicycle Journal, 2022.
Spin-up electron:
The relative direction of circular polarization (left or right) of the electron‘s internal rotating photon determines whether it is a spin-up or spin-down particle. Whichever direction is considered ‘up,’ the other will be considered ‘down.’ This results in a simple and binary relative spin reality for electrons.
See Spin.
References: A. Benn, J.G. Williamson, ‘The Photonic Topology Of Sub-Quantum Spin’, Quicycle Journal, 2022. Arnie Benn: The Physics Of Sub-Quantum Spin, followed by this Q&A.
Sub-Quantum Gravity:
(See Gravity)
Sub-Quantum Mechanics:
An absolutely relativistic quantum mechanics that does not begin with the particle as an axiom, but investigates the substructure of subatomic particles that give rise to their properties. It was developed by John G. Williamson and Martin B. van der Mark, and is encapsulated by the Williamson equation 𝒟𝜇𝚵𝒢 = 0, where 𝒟𝜇 is a Dirac-Clifford four-vector derivative, and 𝚵𝒢 is the root-energy in sixteen spacetime forms including a Lorentz-invariant scalar ‘point’ mass–energy. It has been named the Mathematics of Absolute Relativity Theory (M.A.R.T.), and it is represented by this equation, as well as the concept of quantum inversion. (For a detailed presentation on the subject by John Williamson, see VIDEO: Absolute Relativity Theory: A Proposed Solution To Hilbert’s 6th.)
Even though everything is spin-quantized (in units of ℏ or ½ℏ), in which case there is no such thing as ‘sub-quantum,’ we like the term for two reasons. First, it evokes the idea of delving within subatomic particle structure, and second, it differentiates this model from traditional relativistic quantum mechanics.
Superstrong Force:
The stupidly-strong force holding the electron together. (Formerly known as the ‘Poincaré stresses.’) If you doubt it, smash an electron into a proton at high GeV and see who’s left standing. Unscathed.
We might understand this force as being the result of a powerful form of electro-magnetic and quantum spin coherence — one involving a light-speed gyroscope of electromagnetic energy.
References: J.G. Williamson, M.B. van der Mark, ‘Is The Electron A Photon With Toroidal Topology?’, Annales de la Fondation Louis de Broglie (1997) J.G. Williamson, ‘A New Linear Theory Of Light And Matter’, J. Phys. (2019) J.G. Williamson: Unifying the electron’s particle and wave natures
T
Time (t):
A quantity measured in terms of the regular vibrations or oscillations — the frequency — of a harmonic system. Typical examples include using the revolutions of the Earth around the Sun to designate a year, or the vibrations of a cesium atom in an atomic clock to designate a second. The reason that time is measured in seconds (s) is because frequency is measured in “per second”s (s-1), and an event’s duration is the inverse of how frequently it occurs.
Time is also not a separate ‘thing,’ but is intimately interconnected with the concept of space (see spacetime). Since all radiation and matter in the universe are made of photons, and since all photons are energy waves of a specific frequency traveling at the speed of light, Relativity will affect our perception of frequency, and therefore, also our perception of the flow of time.
( CLICK HERE to watch a clip of John Williamson explaining ‘time’ on the Demystify Sci podcast.)
V
Valence Electrons:
These are electrons in the outermost shell of the atom. Sodium (Na) has 1 valence electron. Oxygen (O) has 6. Electrons in the inner shells are known as core electrons.
W
Wavelength:
The distance from the beginning of one wave to the beginning of the next — the length of one complete cycle of a wave. With electromagnetic (light) waves, when wavelength (𝜆) increases, frequency (𝜈) decreases, and vice versa. This is because the speed of light (c) is constant, and the three are related by the equation c=𝜆𝜈.
Williamson equation:
𝒟𝜇𝚵𝒢 = 0
It is pronounced “D-mu-Ksi-G equals zero,” where 𝒟𝜇 is a Dirac-Clifford four-vector derivative, and 𝚵𝒢 is the root-energy in its 16 spacetime forms, which includes a Lorentz-invariant scalar ‘point’ mass-energy (see below).
It is a fully relativistic equation containing a set of coupled linear differential equations, and requiring no further relativistic corrections. It is designed to be highly and appropriately constrained, to represent what nature does and to exclude what nature does not do. This is best accomplished with a non-commutative Clifford-Dirac algebra, a quaternion-like algebra, which is essential for accurately representing rotations in four dimensional (x, y, z, and t) spacetime.
This equation lies at the heart of the Mathematics of Absolute Relativity Theory, or MART (see above). (For a short overview of the Williamson equation, see this excerpt from Arnie Benn’s short overview of the mathematics of sub-quantum spin (min: 49:35). For a detailed presentation by John Williamson on the subject, see Absolute Relativity Theory: A Proposed Solution To Hilbert’s 6th.)
The 16 root-energy spacetime forms included within the 𝚵𝒢 term are divided into four 3-dimensional sets and four 1-dimensional sets, yielding 16 dimensions. These 16 dimensions are all (only) different mathematical combinations of the 4 dimensions of spacetime, x, y, z, and t — along with their inverses (x-1, y-1, z-1, and t-1). For example, the dx/dt effect of an electric field upon a charge can also be represented, by way of simplifying its dimensionality, as xt-1.
The 16 root-energy spacetime forms are:
3-dimensional:
αi is vector (potential) (x, y, or z)
αij is the bi-vector magnetic field (xy-1 or yz–1 or zx-1)
α0i is the bi-vector electric field (xt-1 or yt–1 or zt-1)
α0ij is the tri-vector spin ‘field’ (x-1yt-1 or y-1zt–1 or z-1xt-1)
1-dimensional:
α0 is time (t)
αP is ‘pivot‘ (root-mass) — in this model, mass is a dynamic term
α123 is tri-vector, a ‘directed 3-volume’ element (x, y, and z)
α0123 is a ‘quadri-vector’ or pseudo-scalar, a ‘directed 4-volume’ element (x, y, z, and t)
The full expansion of the terms:
By way of example, the highlighted terms above represent the three α0ij quantum spin components.
This underscores the power of this new absolute relativistic sub-quantum mechanics, as well as the dynamical detail to which the Williamson equation allows us to gain access. It takes our understanding of matter and energy to the next level — to the sub-quantum level.
The following diagram represents the mathematical transformations that occur within the dynamics of M.A.R.T.
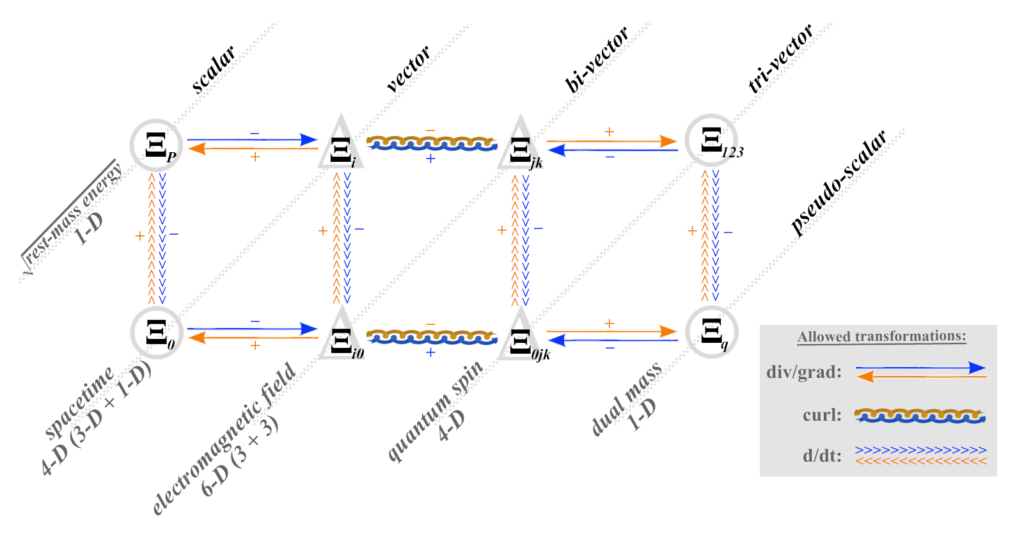
Some loose physical interpretations of the different nodes in the figure above are as follows:
𝚵P (scalar) ‘pivot‘ — root mass-energy — the most basic building block
𝚵0 (vector) time or frequency (or energy when describing quantum systems)
𝚵i (vector) linear delineation of the fabric of space-time’s space in x, y, and z
𝚵i0 (bi-vector) space-time acceleration – Electric Field
𝚵jk (bi-vector) space-space twist – Magnetic Field
𝚵0jk (tri-vector) all three directions of spin
𝚵123 (tri-vector) spherical, radially (in or out) directed volume
𝚵Q (pseudoscalar 𝚵0123) the ‘quedgehog’ — 4-spherical, radially (in or out) directed — contributes to total rest mass
References: J.G. Williamson, A. Benn, M. Rudolph, ‘Quantum Spin Coherence In 4 Derived 3-Spaces’, Quicycle Journal, 2022. J.G. Williamson, ‘A New Linear Theory Of Light And Matter’, J. Phys. (2019) J.G. Williamson, Absolute Relativity Theory: A Proposed Solution To Hilbert’s 6th.