
RETURN to Periodic Table
Below: Electron Shell, Bonding & Ion Formation, Magnetic Properties
Manganese is the 25th element on the periodic table. It has 25 protons and 30 neutrons for a mass of 55 amu, and 25 electrons.
Electron Shell 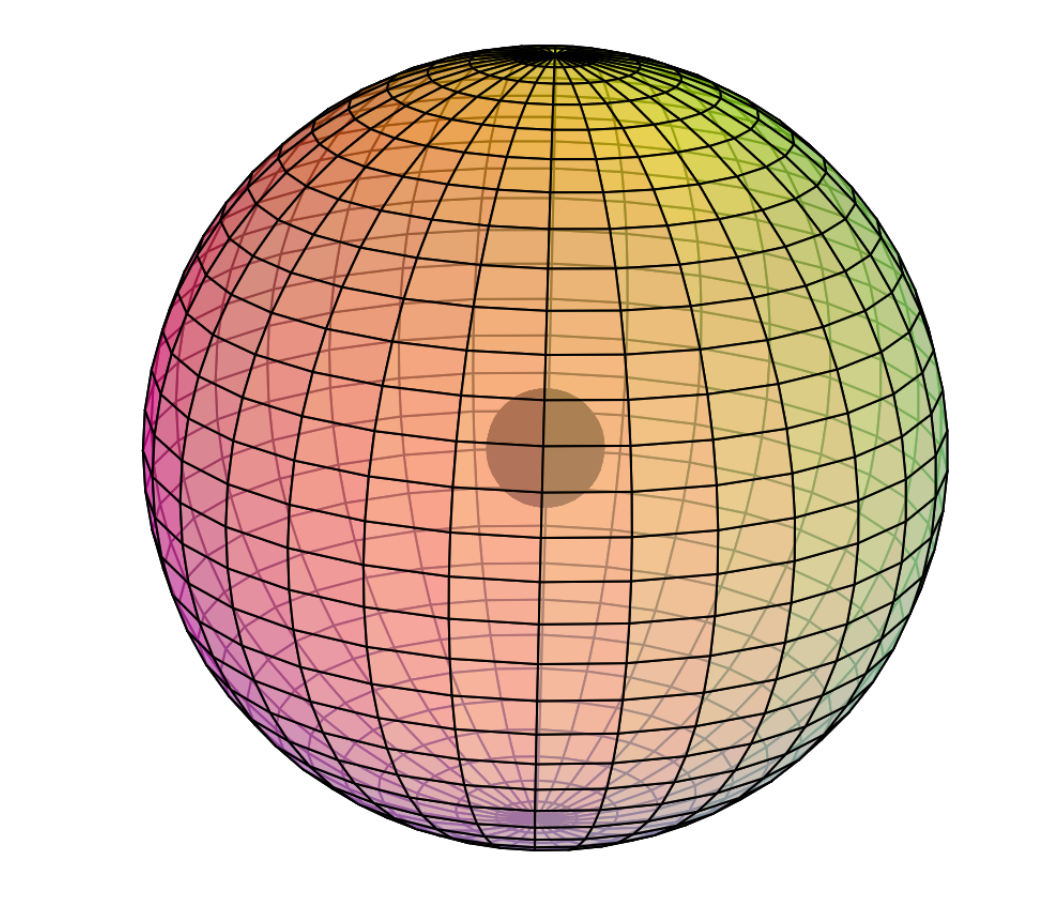
DISCLAIMER: The following reflects the sub-quantum mechanics approach to electron interactions and hybridization. Some details may therefore differ somewhat from traditional quantum chemistry:
Manganese is the fifth element with electrons in the d–orbital. Building upon the pd-hybridization [ref] we introduced in regard to the previous d-block transition metals, it is proposed that manganese, like chromium (Cr), has a 3rd shell containing 3 di-electrons and 5 unpaired electrons in p3d5-hybridized, hexagonal bipyramidal symmetry. The three p-orbital di-electrons occupy three symmetrically distant equatorial positions to minimize repulsion. The 5 unpaired electrons occupy the remaining equatorial and axial positions. An electron from the 4s-orbital is therefore not needed (as it is in the case of chromium) in order to achieve 8-directional symmetry. (See image below.)
This pd-hybridization does not need to involve the 3s-orbital electrons, so they can retain their preferred spherical di-electron state, within which (or upon which) the hybrid orbitals will resonate like harmonics upon a fundamental.
In such a configuration, the 4 tetrahedral 2nd shell di-electrons will align themselves with one di-electron opposite one of the single electrons in the 3rd shell, allowing all other di-electrons to orient their directions roughly between one another in order to minimize repulsion between shells.
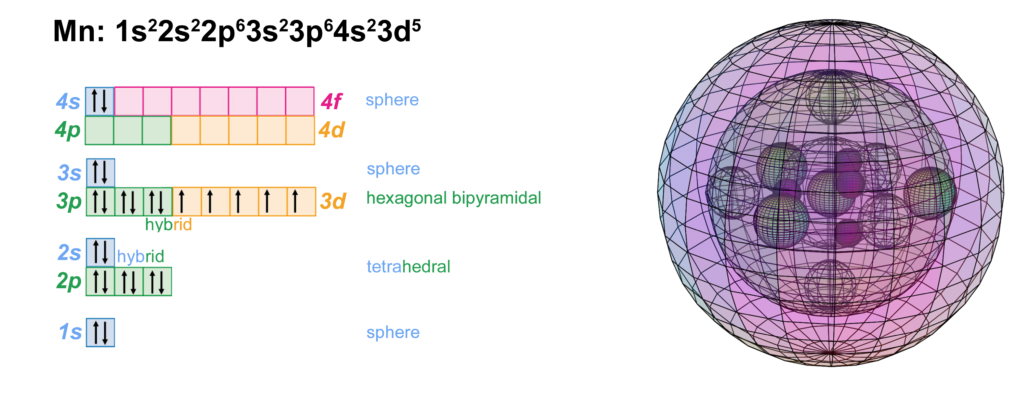
 CLICK HERE to interact with this object
CLICK HERE to interact with this objectNOTE: The small spheres in the image above simply indicate the directions of maximum electron density. The 3rd shell hybrid orbitals themselves will assume a spherical hexagonal bipyramidal structure that divides the 3rd shell into eight roughly equal volumes, with 5-way and 3-way symmetries. Each shell segment will be filled with electron density. It will be highest at the center of the face of each orbital (as in the traditional hybrid orbital lobe shapes) and will decrease toward the nodal regions between orbitals — as wave structures usually do — where electron density will be lowest (though not zero).
NOTE ALSO: Even though it is often useful to talk about these orbitals as separate, they are all — the entire atom is — part of a single, coherent, harmonic, resonant, phase-locked, spherically-symmetrical quantum wave state, and it is all electromagnetic at the root-energy level. Orbitals and their ‘boundaries’ can be seen as nothing more than nodes and antinodes in this harmonic wave structure
The diagram below only shows manganese’s eight 3rd shell p3d5-hybrid orbitals. (The darker color represents di-electrons, the lighter color represents unpaired electrons. The sharp edges should not be taken too literally!)
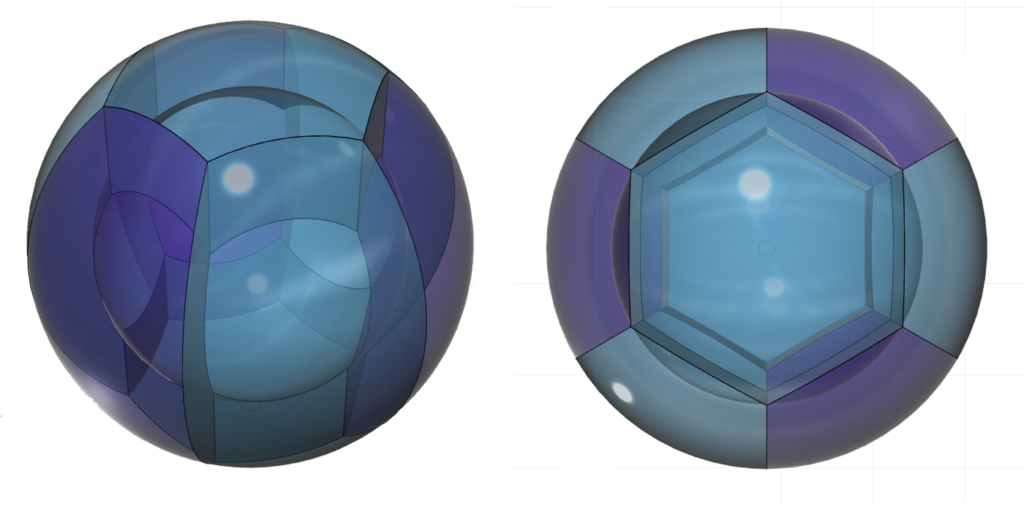
It is also proposed that the stronger repulsion and larger charge density of the three di-electrons will cause them to take up slightly more space and will therefore constrict the five unpaired degenerate electron orbitals slightly. It is expected that this would increase the magnetic signatures of these electrons. (See Magnetic Properties below.)
As in the case of scandium, titanium, vanadium, and chromium, manganese’s 3rd shell p3d5-hybrid orbitals exist within the added sheath of the 3s2-orbital di-electron, since it is not needed for hybridization. It is proposed that they are superimposed within it, as a harmonic frequency coincides with its fundamental frequency in a resonance. It is suggested that the 3s2 di-electron gives additional stability to the electron configuration within it, even though it contains 5 unpaired electrons. The other elements in the d-block will also experience this 3s-orbital stabilization phenomenon, since they achieve at least 4-directional symmetry with only their p– and d-orbitals.
Bonding & Ion Formation 
The 4s2-orbital di-electron shell completes the atom. When forming a metallic crystal, the 4s2 electrons delocalize to form the metallic bond, and when forming a 2+ ion, they are removed. In both cases, the core electron geometry remains the same. (A third ionization, however, would shift its geometry by moving the 2 remaining di-electrons into the axial positions. This assumes that one of the di-electrons will be ionized, rather than an unpaired electron, in order to retain 8-directional symmetry.)
(In a few cases, such as chromium (Cr) and copper (Cu), the 4s-orbital outer shell contains only 1 electron, since the other joins the 3rd shell hybridization within in order to help it achieve 8-directional symmetry.)
Magnetic Properties 
Manganese has a total of five unpaired electrons. In all elements prior to the d-block, unpaired electrons have occurred in the outer (valence) shell of the atom. Those are the electrons involved in chemical reactions. Manganese is the fifth case of an atom with unpaired core electrons. They are protected from reacting (at least, until manganese becomes a Mn2+ ion), and they are stabilized by the 3s di-electron ‘fundamental.’ We propose that it is this protection and stabilization of unpaired core electrons that allows them to interact magnetically, and that consequently determines an element’s magnetic properties.
UNPAIRED CORE ELECTRONS:
While these electrons may technically be called core electrons, for the purposes of this discussion, we recognize that in a metal, if we exclude the valence “conduction” electrons, the pd-hybrid orbital electrons do become ‘valence electrons’ in a sense. Not in the sense that they can participate in chemical reactions, but in the sense that they are now in the outermost shell of the atomic cores, which are suspended in the conduction electron matrix — the 3D electron gas — of the solid metal crystal.
PARAMAGNETISM:
In the presence of an external magnetic field, an unpaired core electron will orient its spin to align with the magnetic field. This will cause the atom to be drawn into and toward that field — via magnetic field cancellation — giving it a positive magnetic susceptibility (χm) value. This attractive force is called paramagnetism, and its effects only last as long as the external magnetic field is present. We might therefore presume that, the stronger the paramagnetism, the more ‘unpaired electron character’ is present. Surprisingly, this does not seem to go according the number of unpaired electrons present, as the diagram below illustrates. There must therefore be other contributing factors, which we will investigate below.
Manganese is the most paramagnetic metal of the 3d row (excluding the ferromagnetic iron, cobalt, and nickel) even though it has fewer unpaired electrons than chromium and more than iron, cobalt, and nickel. (As to the reason that manganese is not ferromagnetic, click HERE .)
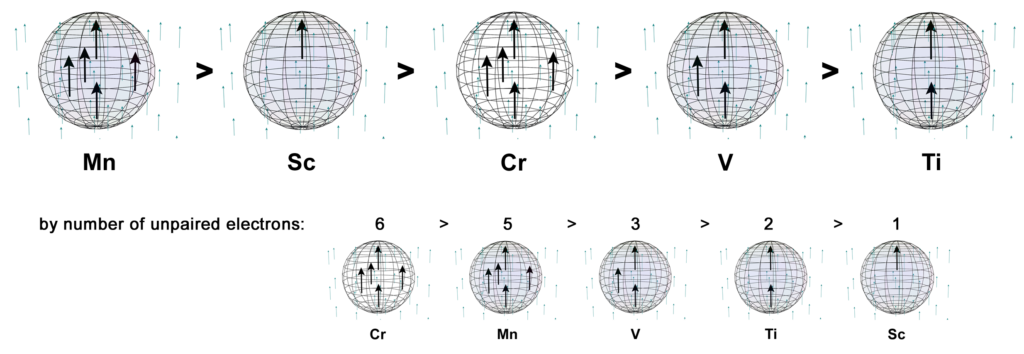
Manganese’s five unpaired electrons are arranged in a hexagonal bipyramidal structure. The images below are intended to represent the orientation of these 5 electrons in an external (or adjacent atom’s) magnetic field (whose north pole is pointing upwards). (The arrows inside the atom represent the unpaired electrons and the black dots represent the relative positions of the di-electrons.)
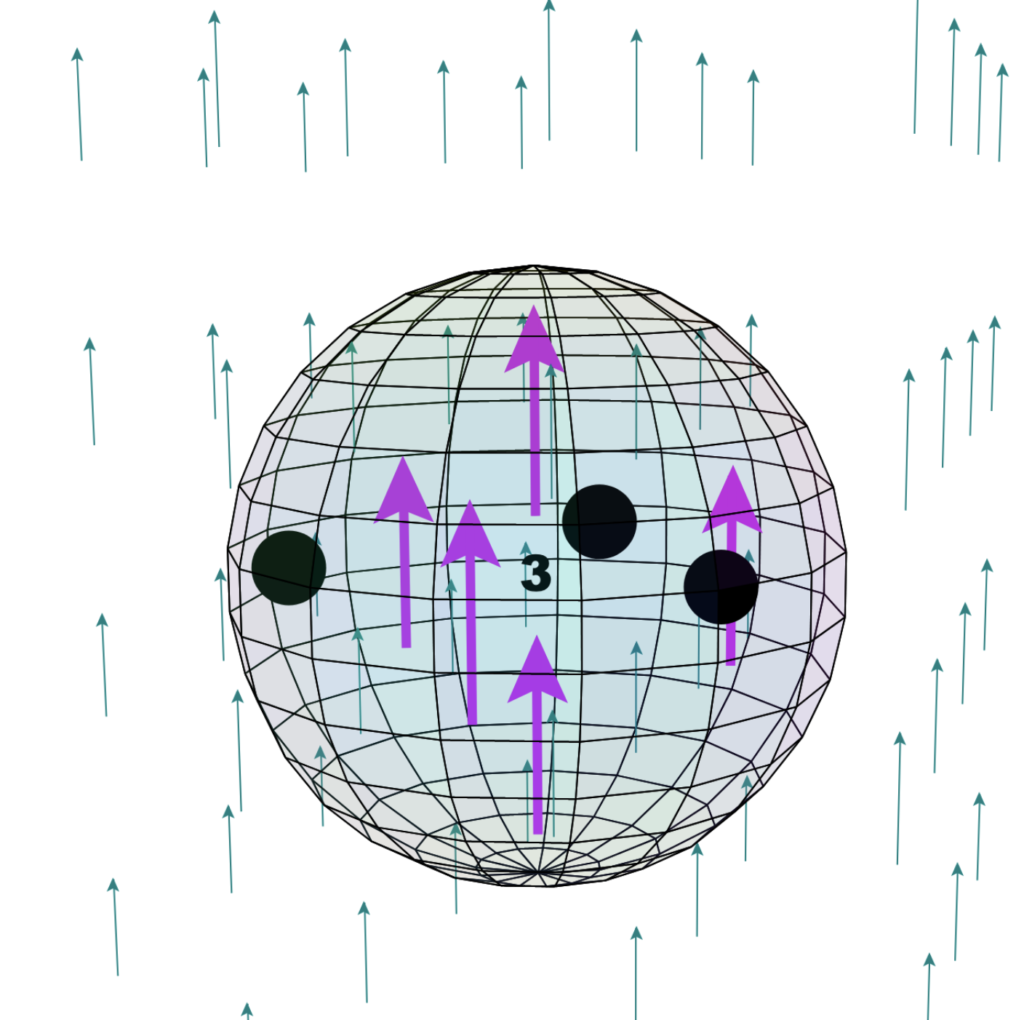
 CLICK HERE to interact with this object
CLICK HERE to interact with this objectManganese has five unpaired electrons, and it therefore makes sense that it should have the highest magnetic susceptibility value (χm = +511) of the (non-ferromagnetic) 3d transition metals. It is here proposed that this is due to the spin bonding and field cancellation that occurs between its five unpaired electrons, given their proximity, degeneracy, and slight orbital constriction.
If we consider scandium’s single unpaired electron to have an EME ≈ 1e– (with χm = +295), and titanium’s 2 linear spin bonding electrons to have an EME ≈ 0.51e– (with χm = +151), along with vanadium’s 3 parallel spin bonding electrons to have an EME ≈ 0.97e– (with χm = +285), and chromium’s 5 linear and parallel spin bonding electrons to have a disrupted EME ≈ 0.57e– (with χm = +167), then manganese’s 5 linear and parallel spin bonding electrons appear to have an EME ≈ 1.73e–. That equates to about 0.35e– of electron signature contributed per electron.
This value of 0.35e– is very similar to vanadium’s 0.32e–, and when we compare the two geometries, there is an interesting similarity. The three hybrid unpaired-electron orbitals in vanadium are at 90° to one another, and in a planar arrangement through the atom. In the orbital structure of manganese (and chromium), this same planar, 90° relationship exists — except that there are three iterations of it (if we consider three axial sections). In all three cases, there are also 3 di-electrons in the shell, similarly constricting the unpaired electron orbitals. Each of these iterations should manifest a similar amount of electron energy reduction due to spin bonding, given the geometric similarity.
We might therefore expect the ‘per electron’ numbers to be comparable, and they should also shed light on what chromium’s numbers might have been without the single-valence-electron issue. Manganese’s χm value is obviously larger than vanadium’s, though, because it has two more electrons (of roughly the same EME) contributing to its signature.
PARAMAGNETIC STRENGTH ANALYSIS:
The following diagram shows the relative paramagnetic strengths of the transition metals, along with their proposed hybrid orbital geometries. (See paramagnetic strength trend analysis for more detail.)
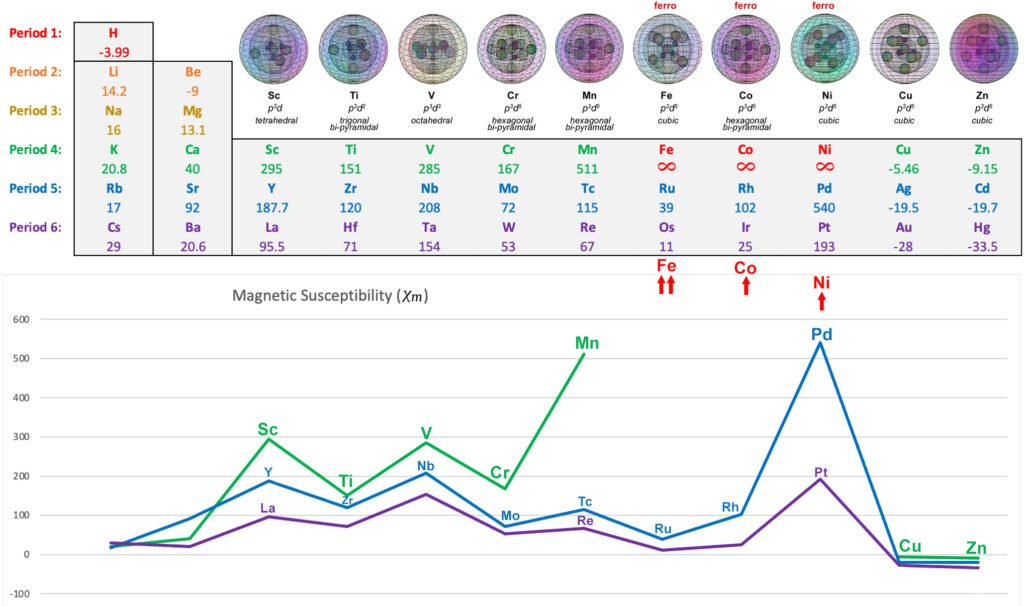
OTHER PARAMAGNETIC 3d METALS: Scandium, Titanium, Vanadium, Chromium (also antiferromagnetic), Manganese
FERROMAGNETIC 3d METALS: Iron, Cobalt, Nickel
DIAMAGNETIC 3d METALS: Copper, Zinc
RETURN to the Periodic Table
