28. Nickel - The Quantum Bicycle Society

RETURN to Periodic Table
Below: Electron Shell, Bonding & Ion Formation, Magnetic Properties

Nickel is the 28^th element on the periodic table. It has 28 protons and 31 neutrons for a mass of 59 amu, and 28 electrons.

Electron Shell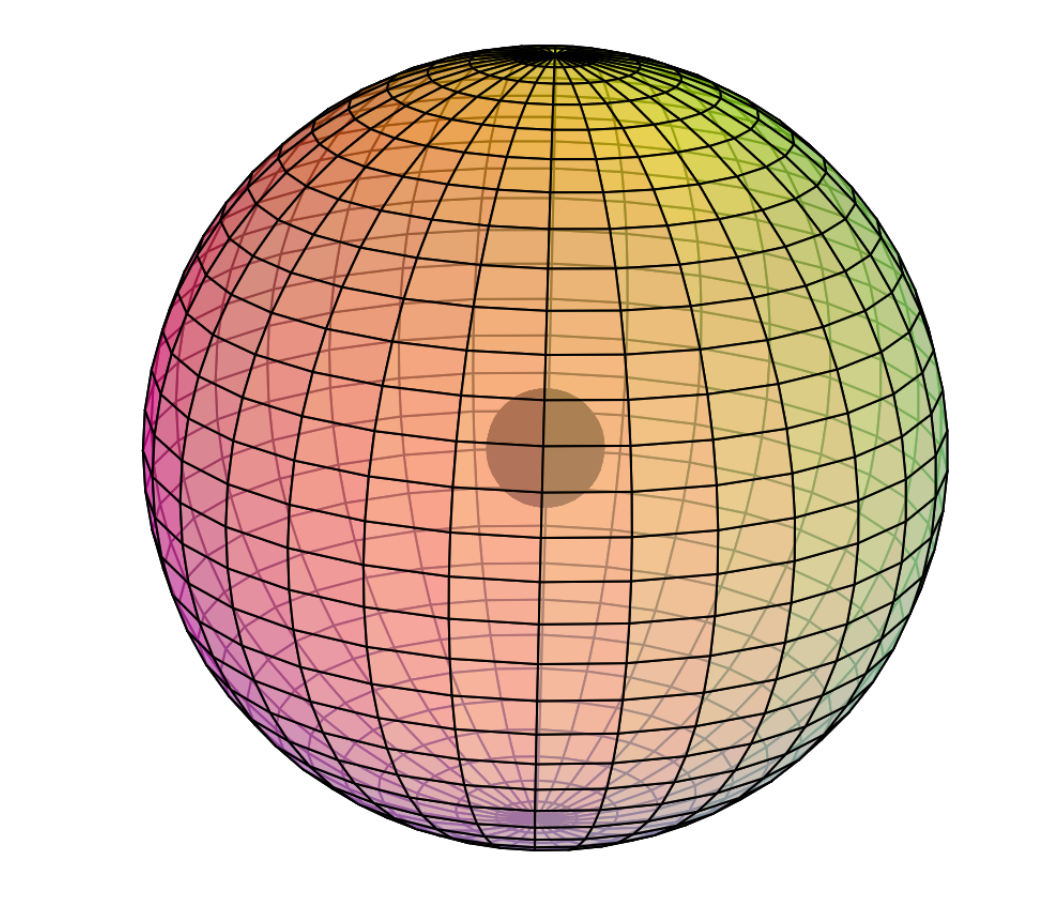

DISCLAIMER: The following reflects the sub-quantum mechanics approach to electron interactions and hybridization. Some details may therefore differ somewhat from traditional quantum chemistry:

Nickel is the eighth element with electrons in the d–orbital. Building upon the pd-hybridization [ref] we introduced in regard to the previous d-block transition metals, it is proposed that nickel has a 3^rd shell containing 6 di-electrons and 2 unpaired electrons in p³d⁵-hybridized, cubic symmetry. The 2 unpaired electrons will occupy two opposite corners in the cubic configuration. This structure (shown below from two perspectives) can also be viewed as two intersecting, antiparallel (and antiprismatic) tetrahedra with one electron in each occupying the two opposite ‘axial’ positions.

In such a case, one of the 4 tetrahedral 2^nd shell di-electrons will align itself opposite one of the single electrons in the 3^rd shell, allowing all other 2^nd and 3^rd shell di-electrons to orient their directions roughly between one another in order to minimize repulsion between shells.

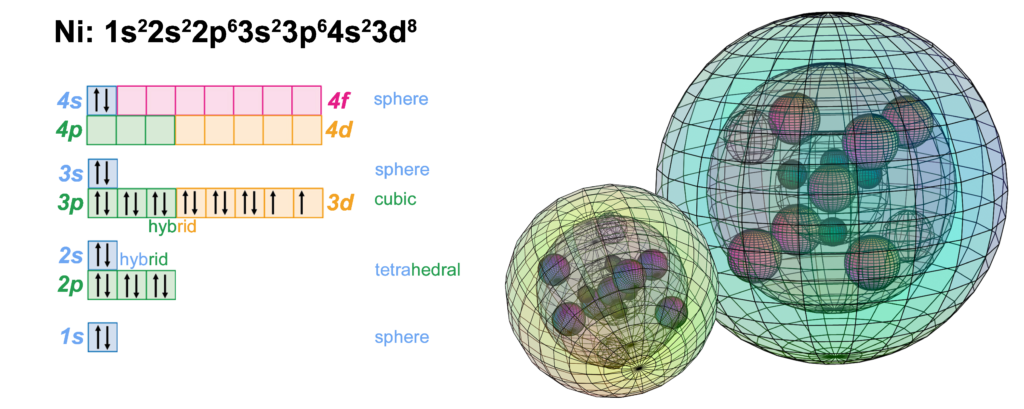
CLICK HERE to interact with this object

NOTE: The small spheres in the image above simply indicate the directions of maximum electron density. The 3^rd shell hybrid orbitals themselves will form a cubic arrangement that divides the (cuboctahedral) shell into eight equal volumes, with a 6-way and a 2-way symmetry. The entire shell will be filled with electron density. It will be highest at the center of the face of each orbital (as in the traditional hybrid orbital lobe shapes) and will decrease toward the nodal regions between orbitals — as wave structures usually do — where electron density will be lowest (though not zero).

NOTE ALSO: Even though it is often useful to talk about these orbitals as separate, they are all — the entire atom is — part of a single, coherent, harmonic, resonant, phase-locked, spherically-symmetrical quantum wave state, and it is all electromagnetic at the root-energy level. Orbitals and their ‘boundaries’ can be seen as nothing more than nodes and antinodes in this harmonic wave structure.

The diagram below shows only nickel’s eight 3^rd shell p³d⁵-hybrid orbitals. (The darker blue color represents di-electron orbitals, the lighter blue color represents unpaired electron orbitals.) In reality, the eight volumes will not be exactly equal in size because di-electron orbitals (with charge 2-) will be larger and will repel the unpaired electron orbitals (with charge 1-) more strongly, constricting them. It is therefore proposed that nickel’s unpaired electron orbitals will form a linear (axial) geometry with respect to one another, due to the symmetry of the constriction around (and between) them, and that they will become extended, radially outward, as a result of its magnitude, as well as the repulsion from the 2^nd shell beneath them.

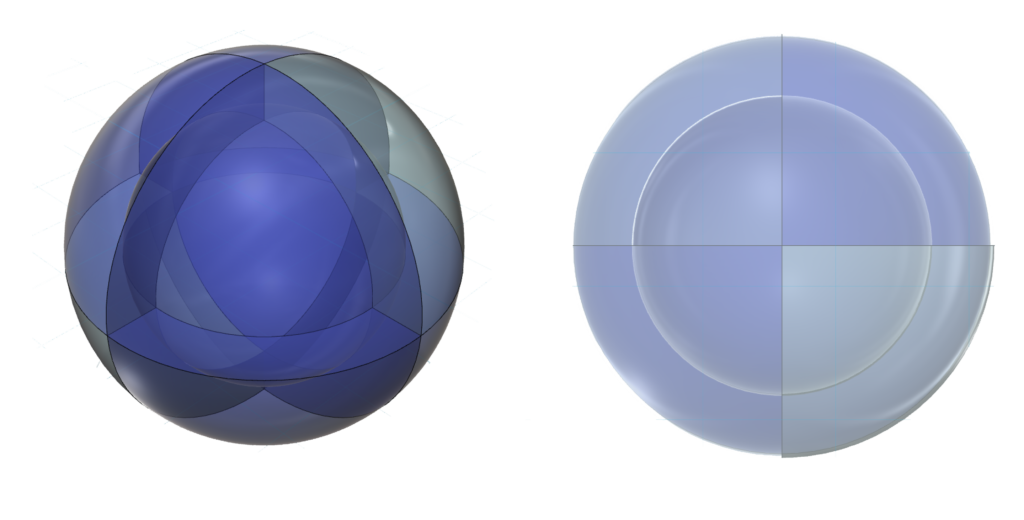
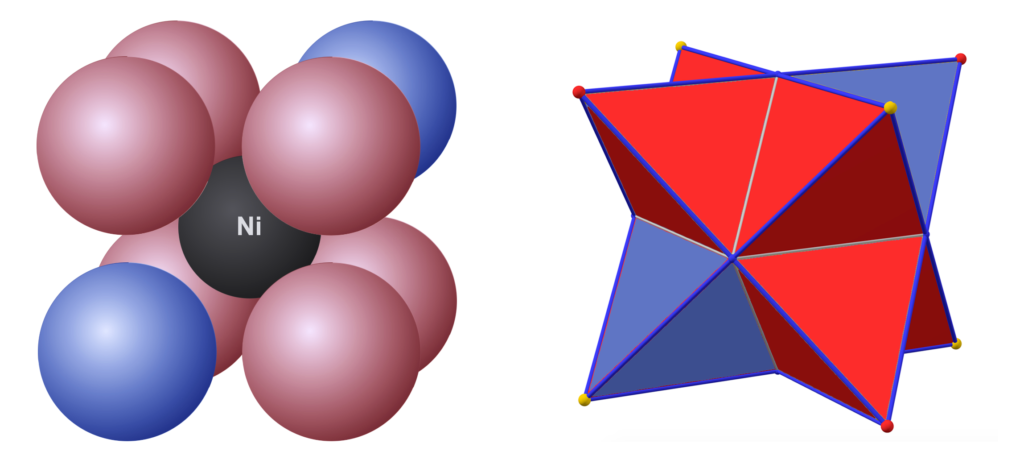
*Fig. 2: Nickel’s 3^rd shell cubic 2-electron and 6-di-electron configuration. Oblique view (left) and top view (right).*

Although nickel’s electron geometry is effectively linear, the double antiparallel tetrahedral symmetry of its 3rd shell is also known as a dual tetrahedron, in which each point also coincides with a corner of a cubic structure. Two different views of this are offered below.

Fig. 3: ‘Cubic’ view of a nickel atom’s eight 3^rd shell p³d⁵-hybrid orbitals around the atomic core (black), along with a dual tetrahedron formed from two ‘antiparallel’ (antiprismatic) intersecting tetrahedra.

Bonding & Ion Formation

When nickel atoms bonds with other metal atoms in a solid, they form a crystal structure in which their valence electrons become ‘delocalized’ — shared into a matrix of electron density within which the now-positive atomic cores remain suspended. They are held in their relative positions by a balance between attraction into the electron gas around them and repulsion from the adjacent positive atomic cores. This is the electrostatic nature of metallic bonding. Its electron delocalization is also the reason that metals are such good conductors of both heat and electrical potential.

When nickel interacts ionically, it usually makes the Ni²⁺ ion, though there are other possibilities (such as the Ni³⁺ or Ni⁴⁺ ions). The Ni²⁺ ion forms when the atom loses its 4s² valence electrons. The Ni³⁺ ion forms when the Ni²⁺ ion loses another electron. It is here proposed that the 3^rd electron will be lost from one of the 3^rd shell di-electrons, since this is the only way to retain 8-directional symmetry. The Ni³⁺ ion will therefore achieve the same (hexagonal bipyramidal) electron configuration we saw in cobalt (Co) and manganese (Mn), though without any 4s-electron density. The Ni⁴⁺ ion will therefore achieve the same (cubic) electron configuration we saw in iron (Fe).

In ionic crystals — without delocalized electron density — nickel ions no longer conduct electricity. They will, however, still be magnetically active because they still hold unpaired electrons. While metallic nickel is ferromagnetic (see below), nickel ions will be strongly paramagnetic.

Magnetic Properties

Iron (Fe), cobalt (Co), and nickel (Ni) are ferromagnetic, though nickel is the least ferromagnetic of the three. (See Magnetism for more detail.)

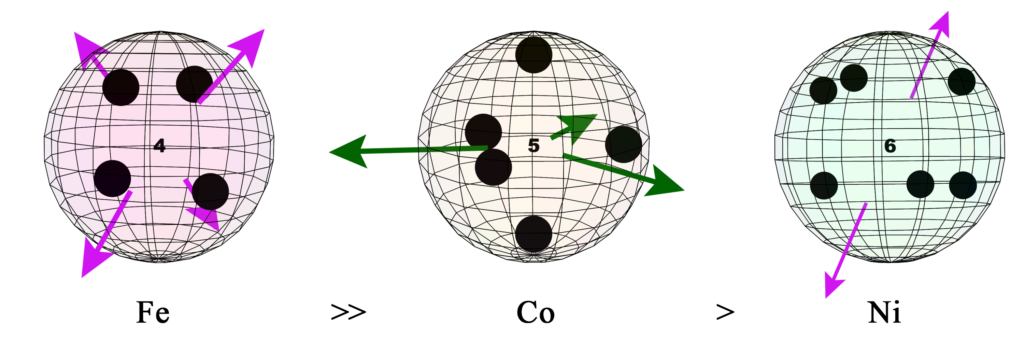
*Fig. 4: Ferromagnetic strength trend in the metals of the 3d-block.*

UNPAIRED CORE ELECTRONS:
The presence of unpaired core electrons determines an element’s magnetic properties. While these electrons may technically be called core electrons, for the purposes of this discussion, we recognize that in a metal, if we exclude the valence “conduction” electrons, the pd-hybrid orbital electrons do become ‘valence electrons’ in a sense. Not in the sense that they can participate in chemical reactions, but in the sense that they are now in the outermost shell of the atomic cores, which are suspended in the conduction electron matrix — the 3D electron gas — of the solid metal crystal.

Unpaired core electrons are protected from reacting with other atoms. They are held in their geometry by atomic orbital constraints, they are kept from pairing up with each other by the spin and field exclusion of degeneracy, and it is proposed that they are stabilized by the presence of the 3s² orbital ‘fundamental’ [ref].

PARAMAGNETISM:
Protected unpaired core electrons are, however, still free to respond to and orient themselves with an external magnetic field. In doing so, they cancel magnetic field with that external field (through destructive interference), which lowers energy and attracts them towards the field. The paramagnetic atom as a whole is then attracted, along with these electrons, towards the magnetic field — attracted equally to the ‘north’ as to the ‘south’ polarity. This is called paramagnetism, and it is an expected property of metals with unpaired core electrons.

When the external field is removed, the electron spins within adjacent paramagnetic atoms return to their previous, random distribution. (See paramagnetic strength trend analysis for more details.)

FERROMAGNETISM:
As we discussed regarding iron (Fe) and cobalt (Co), however, ferromagnetism occurs when the electrons in a substance are able to retain their internal crystalline magnetic field alignment after the external field that aligned them is removed. The solid can then act as a permanent magnet. This property therefore depends directly upon how well the unpaired electrons on adjacent atoms can link their spins and magnetic fields, thereby holding one another in alignment.

It is here proposed that there are two criteria that are required in order for the atoms of a metal crystal to achieve ferromagnetic spin bonding, and thus, a crystal-wide ferromagnetic spin resonance.

CRYSTAL GEOMETRY: For optimal spin bonding, unpaired core electrons should have an electron domain geometry that matches the crystal unit cell geometry. We propose that the 8-directional symmetries that arise as a result of pd-hybridization may provide these.
SUFFICIENT ORBITAL EXTENSION: Unpaired core electrons require constriction and radial extension in order to interact (via spin bonding) with similarly extended core electrons on adjacent atomic cores in a crystal. We propose that this is achieved as a result of sufficient di-electron (electron pair) repulsion within the atomic shell, along with added repulsion from the di-electrons in the 2^nd shell that lie directly beneath the unpaired core electron orbitals. This criterion is therefore intimately related to the electron geometry (from criterion #1 above), as well as to the number of same-shell di-electrons constricting the unpaired electron orbitals.

Only with both of these criteria fulfilled (see below), will a transition metal be ferromagnetic. If only one is present, or if constriction and extension are not sufficient, the element will be paramagnetic.

CRITERION #1: NICKEL’S CRYSTAL GEOMETRY:
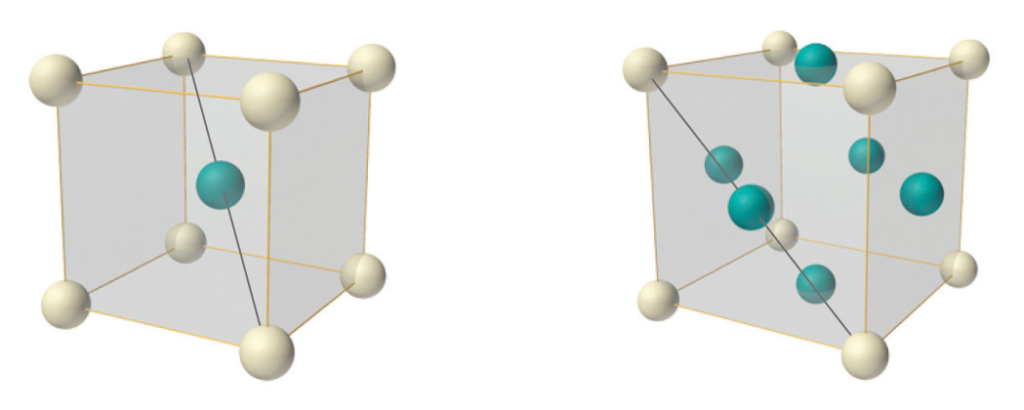
Nickel is ferromagnetic below its Curie Temperature (of 354°C), and has a face-centered cubic (FCC) crystal structure. When heated past its Curie Temperature, it loses its ferromagnetism in favor of paramagnetism.

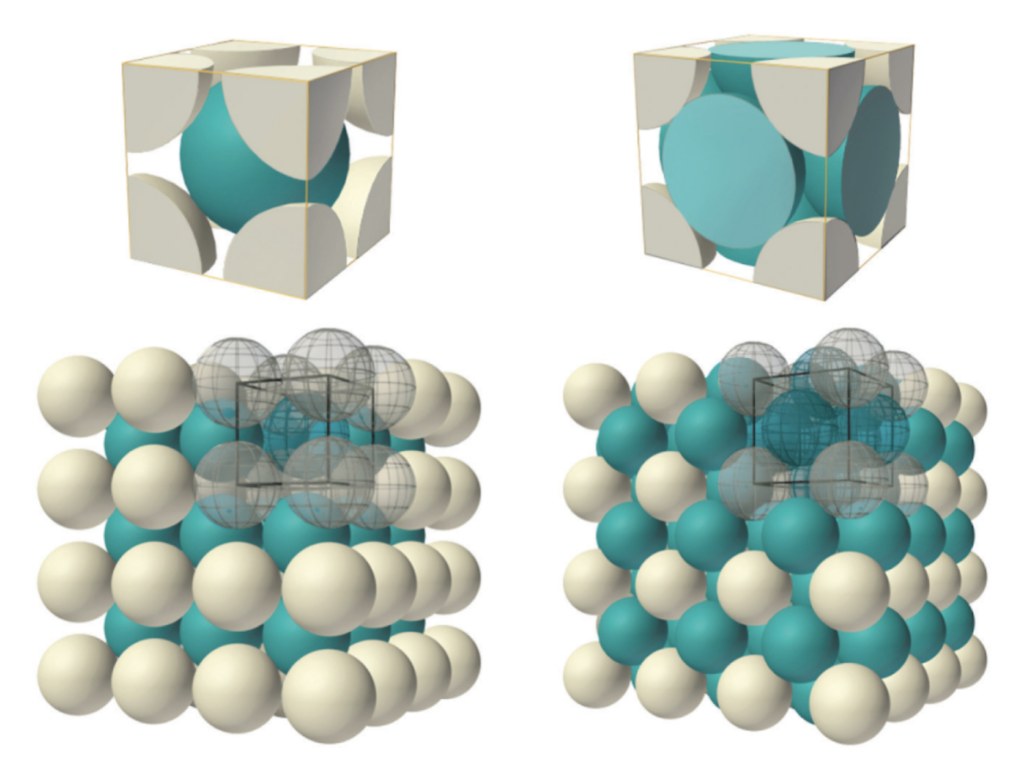
*Fig. 5a: Diagrams of iron’s BCC body-centered cubic (left) and nickel’s FCC face-centered cubic (right) crystal structures.*

In a FCC crystal (above, right), each atom has 12 nearest neighbors. These nearest neighbors lie on the diagonals of the faces of the FCC unit cell (top right, above). As such, the tetrahedral crystal geometry proposed for iron (Fe) would not align in this “45º” paradigm. It would, however, allow for atoms with linear spin interactions to align.

*Fig. 5b: Diagrams of iron’s tetrahedral BCC nearest neighbor relationship (left) and nickel’s linear FCC nearest neighbor relationship (right)*

Since it is proposed that nickel has a linear geometry of unpaired electron orbitals, an FCC crystal structure (above, right) may allow for an effective spin bonding resonance to align within a nickel crystal.

A clear shortcoming of this electron structure is that, while it may facilitate the correct geometric alignment for ferromagnetic spin bonding in nickel, there are only two unpaired electrons spin bonding per atom, as opposed to four in the case of iron. As such, it makes sense that the ferromagnetism of nickel would be far weaker than that of iron, resulting in a more easily-disrupted ferromagnetic spin resonance and a lower Curie Temperature.

CRITERION #2: SUFFICIENT ORBITAL EXTENSION:
As was proposed above, though, the alignment of spin and field is not enough to effect a ferromagnetic resonance on its own. Since these are interactions between core electrons, their influence (and connections) need to be sufficiently enhanced and extended outward from the atomic cores in order to be felt by adjacent atoms in the crystal, and to facilitate ferromagnetic spin bonding.

In addition to nickel’s 2 linear unpaired electrons, its 3^rd shell also contains 6 di-electrons. (These are depicted by large black dots in fig. 6 below, and by the “6” in its center). Furthermore, 1 of the 4 di-electrons in the 2^nd shell is aligned directly beneath one of the unpaired electrons of the 3^rd shell.

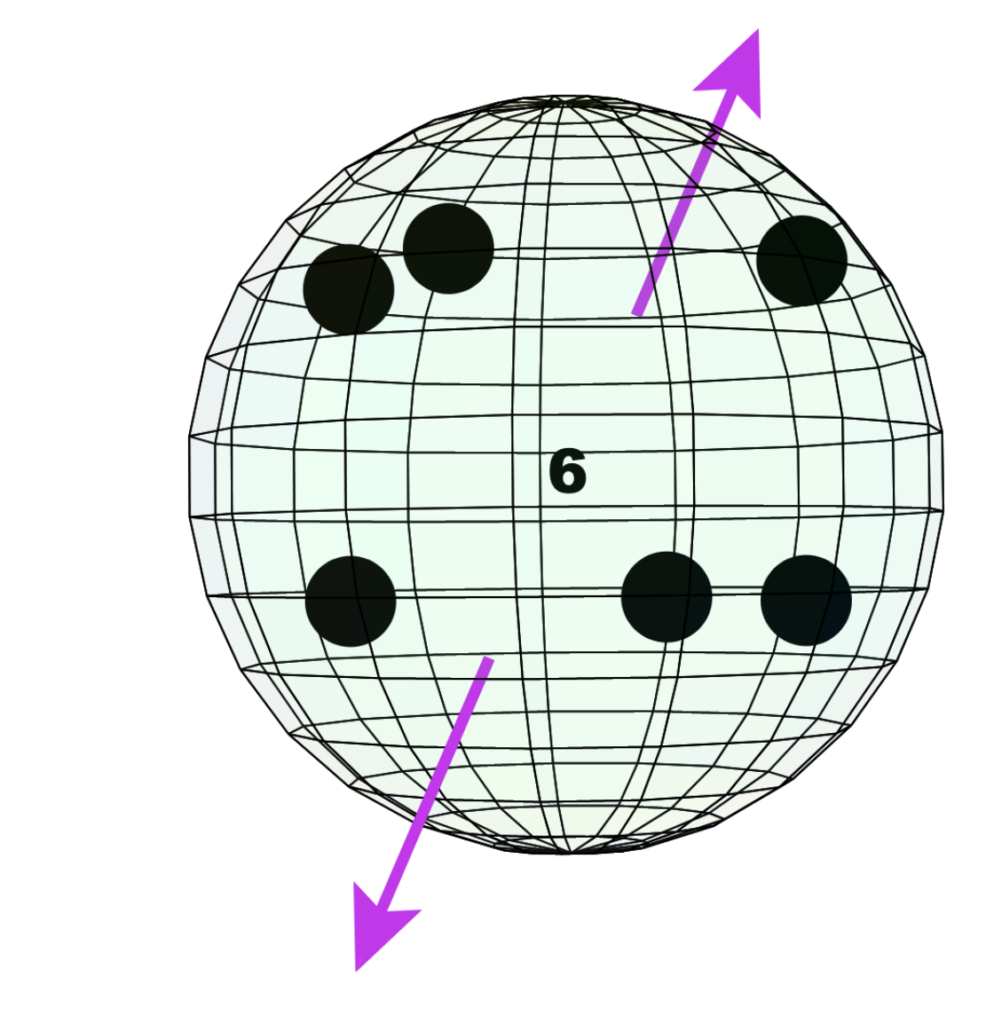
*Fig. 6: Nickel’s extended core unpaired electron orbitals*

Di-electron orbitals are larger than unpaired electron orbitals, and they have double the charge. They therefore repel unpaired electron orbitals more strongly. It has been proposed that this can not only constrict the unpaired electron orbitals but also cause them to become extended, radially outward, from the atomic core. In the case of nickel, the unpaired electron orbitals are experiencing this form of constriction from 7 di-electrons — 6 from beside/around them in the same shell, and 1 from beneath them in the 2^nd shell.

It is proposed that the combination of all this di-electron repulsion forces the influence of nickel’s unpaired electron orbitals to be extended significantly further outward (just as a spinning cylinder, forced to become thinner, that responds by becoming longer). This extends the influence of these electrons’ spins and magnetic fields into the electron gas around the atomic cores (as shown in fig. 6, above), and it is suggested that this is what makes electron spin interactions between adjacent crystalline nickel atoms possible. [Ref]

For more on the relative trend in ferromagnetic strength, see Magnetism & Magnetic Trends.

PARAMAGNETIC 3d METALS: Scandium, Titanium, Vanadium, Chromium (also antiferromagnetic), Manganese
OTHER FERROMAGNETIC 3d METALS: Iron, Cobalt, Nickel
DIAMAGNETIC 3d METALS: Copper, Zinc