Magnetism & Magnetic Trends
This page will consider several concepts related to magnetism from the point of view of sub-quantum mechanics, factoring in its perspective on electron interactions in magnetic field space and spin space. The 3rd-shell transition metals will be compared, and the concept of pd-hybridization will be employed, in an attempt to account for the periodic trend in magnetic susceptibility (χm) strength.
Below, we will briefly address the nature and mechanisms behind:
- MAGNETISM: What is it, really?
- PARAMAGNETISM: What causes temporary magnetic attraction?
- PARAMAGNETIC STRENGTH: What accounts for its periodic trend?
- DIAMAGNETISM: Temporary magnetic repulsion and its periodic strength trend.
- FERROMAGNETISM: What causes permanent magnetic attraction?
- FERROMAGNETIC STRENGTH: What accounts for its periodic trend?
- CURIE TEMPERATURE TREND: Why do they lose magnetism in that order?
- WHY ONLY THESE THREE?: Why are only Fe, Co, & Ni ferromagnetic?
- ANTIFERROMAGNETISM: What causes equal and opposite alignment?
- OTHER FORMS OF MAGNETISM
1. What Is Magnetism?
Magnetism can be understood as a force of attraction or repulsion resulting from the flow of electric current or the spin of a charged particle.
According to both the Williamson-van der Mark and Robinson models, subatomic particles are made of self-confined knots of electromagnetic radiation, and as such, they cause electric and magnetic fields to be introduced into the spacetime around them.
In the toroidal, double-loop rotation of the electron [ref], for example, chirality is immediately a characteristic of the system, and this naturally divides ‘spin reactions’ (magnetism) into two complementary forms that we call north and south. They are simply the two relative chiral orientations of the rotating electromagnetic flow. By way of example, Earth’s rotation will appear right-handed (counter-clockwise) when viewed from above the north pole, but left-handed (clockwise) when viewed from above the south pole.
In an electron, the (instantaneous) north magnetic pole lies along the axis running through the center of the toroidal topology, in the direction of the thumb in a left-handed chiral rotation. South lies in the opposite direction along the same axis. In an isolated electron, the magnetic field averages to zero (due to the electron’s spherically-symmetrical spin). The magnetic moment of the electron emerges only in the presence of an external field, which breaks the internal spherical symmetry of the isolated electron. (According to this model, a positron has the same topology, but with a right-handed chirality (as shown below, right), which is what gives it the opposite charge.)
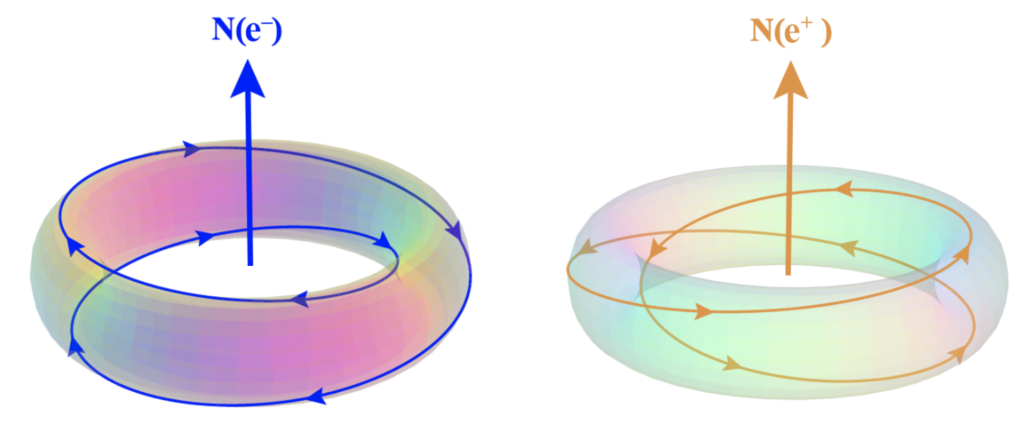
(The above images are of photon topologies in momentum space, and as such, they should not be taken too literally. See Understanding electrons for more.)
When the (magnetic field) influence of a particle’s spin is extended into the spacetime around it, other magnetic fields respond to it when they encounter it. The magnetic fields of other nearby electrons will therefore interact with this electron’s field in such a way that north repels north but attracts south. This ultimately derives from the fact that angular momenta are either working together, ‘counter-rotating’ in balance and lowering energy (attraction), or ‘co-rotating’ in such a way that increases energy (repulsion). [Ref]
An unpaired electron therefore has a magnetic field as a result of its spin and its internal toroidal photon topology. (Similarly, its electric charge arises from the topology of the photon’s electric field.)
When many (unpaired) electrons exist in concert, for instance within a solid crystal, various different forms of magnetism can result, depending upon the geometry of and the interactions between these electrons. Some of these forms of magnetism will be discussed below.
The most well-known form is ferromagnetism (see below), in which the unpaired electrons throughout a metal crystal align their magnetic spins, and are able to hold this crystal-wide alignment. The crystal as a whole then manifests a macro-magnetic field, becoming a permanent ‘ferromagnet.’ The most important example of this occurs in iron (Fe).
When electrons (with opposite spins) pair up, on the other hand, they superimpose in a way that finds them perfectly anti-parallel. This allows their magnetic fields to cancel against one another, which lowers energy significantly, making this a highly favorable state. One example of this is the electron shell of a helium (He) atom. Due to its internal magnetic field cancellation, this di-electron pair is no longer attracted towards other magnetic fields, but rather, repels them. This is called diamagnetism (see below), and it happens in order to maintain the pair’s lowest energy state of perfect field cancellation.
2. Paramagnetism
The presence of unpaired core electrons determines an element’s magnetic properties. While these electrons may technically be called core electrons, for the purposes of this discussion, we recognize that in a metal, if we exclude the valence “conduction” electrons, the pd-hybrid orbital electrons do become ‘valence electrons’ in a sense. Not in the sense that they can participate in chemical reactions, but in the sense that they are now in the outermost shell of the atomic cores, which are suspended in the conduction electron matrix — the 3D electron gas — of the solid metal crystal.
In the presence of an external magnetic field, an unpaired core electron will orient its spin to align with the magnetic field. This will cause the atom to be drawn into and toward that field — via magnetic field cancellation — giving it a positive magnetic susceptibility (χm) value. This attractive force is called paramagnetism, and its effects only last as long as the external magnetic field is present. We might therefore presume that, the stronger the paramagnetism, the more ‘unpaired electron character’ is present. Surprisingly, this does not seem to go according the number of unpaired electrons present, as the diagram below illustrates. There must therefore be other contributing factors, which we will investigate below.
3. Paramagnetic Strength Trend
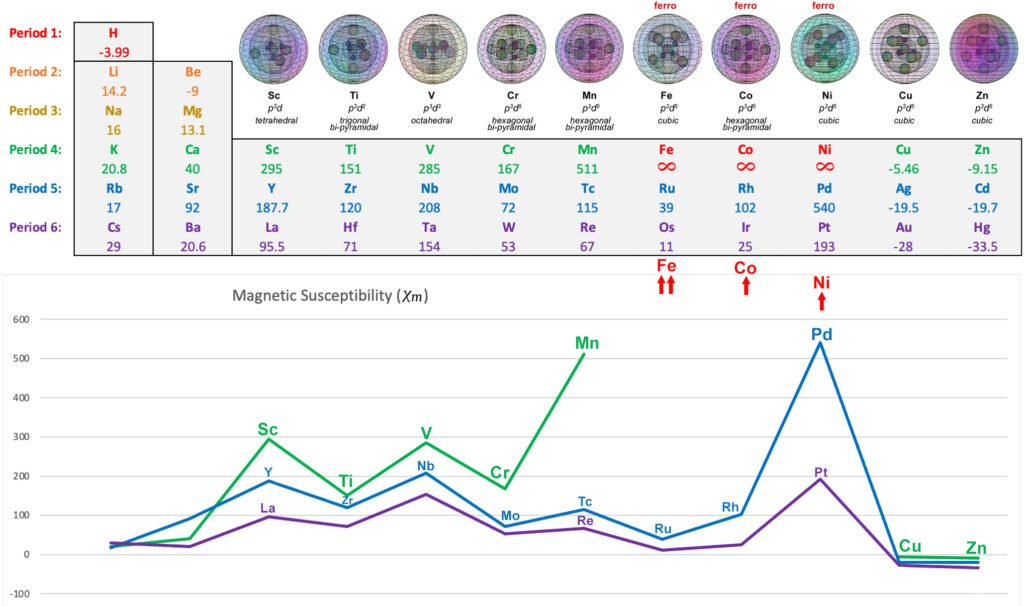
The following diagram shows the relative paramagnetic strengths of the transition metals, along with their hybrid orbital geometries.
Several questions immediately present themselves: Why does scandium (Sc) have a higher paramagnetic strength with 1 unpaired electron than vanadium (V) has with 3 unpaired electrons? Why does palladium (Pd) (with supposedly no unpaired electrons) have a higher value than manganese (Mn) with 5 unpaired electrons?
ANALYSIS:
Below is a summary of some of the detail that can be found on the periodic table listing for each of the transition metal elements.
Scandium (Sc):
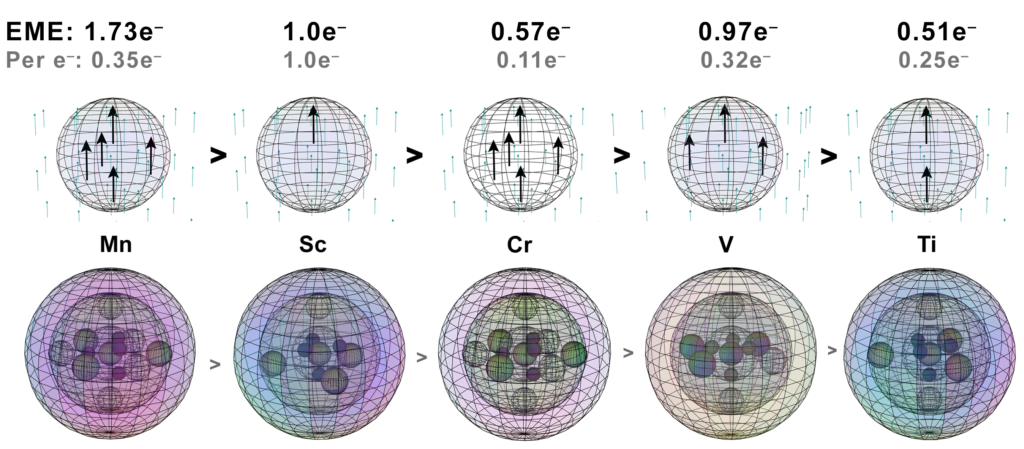
Scandium has 1 unpaired core electron, no mitigating electron resonance, and a magnetic susceptibility value of χm=+295. We might therefore consider this the value for the effective magnetic electron (EME) signature of a single electron: EME≈1.0e–.
(See scandium (Sc) for more detail.)
*
Titanium (Ti):
Titanium has 2 unpaired core electrons in an axial, linear alignment. This reduces its magnetic susceptibility value by about half, down to χm=+151. This might then represent an EME≈0.51e–. We might understand this as a result of the energy reduction associated with linear spin bonding and field cancellation (via destructive interference) taking place between these unpaired core electrons within the atomic core. We might understand this as meaning that each of the 2 spin-bonding electrons has been reduced to a contribution of EME≈0.25e–.
(See titanium (Ti) for more detail.)
*
We might next consider how the geometries of vanadium and manganese might reflect variations upon this theme. (Chromium will be considered last since it is a variation on the geometry of manganese.)
*
Vanadium (V):
Vanadium has 3 unpaired core electrons. Two are in an axial, linear alignment, with the third electron domain lying between them and orthogonal to them — three adjacent lobes in a planar arrangement within an octahedral symmetry.
In this case, there are three electrons spin bonding together, but this time they are parallel spin bonding adjacent to one another. We might expect that this would increase the coherence of the spin bonding and decrease EME. On the other hand, the unpaired electrons are also being compressed together by the repulsion of 3 di-electron orbitals in the same shell, which should increase their EME. As such, it makes sense that each of vanadium’s electrons might contribute a diminished EME, though not quite as diminished as in the case of titanium.
Vanadium has a magnetic susceptibility value of χm=+285, which would represent an EME≈0.97e–. We might understand this as meaning that each of the 3 spin-bonding electrons contributes an EME≈0.32e–, slightly more than in the case of titanium.
(See vanadium (V) for more detail.)
*
Manganese (Mn):
Manganese has 5 unpaired core electrons. Two are in an axial, linear alignment, and 3 occupy a trigonal planar distribution in the equatorial plane — five adjacent lobes within a hexagonal bipyramidal symmetry. This arrangement has the effect of producing a magnetic susceptibility value of χm=+511, which would represent an EME≈1.73e–. We might understand this as meaning that each of the 5 spin-bonding electrons contributes an EME≈0.35e–, very similar to the case of vanadium.
When we compare the two geometries, there is an interesting similarity. The three hybrid unpaired-electron orbitals in vanadium are at 90° to one another, and in a planar arrangement through the atom. In the orbital structure of manganese (and chromium), this same planar, 90° relationship exists — except that there are three iterations of it (if we consider three axial sections). In all three cases, there are also 3 di-electrons in the shell, similarly constricting the unpaired electron orbitals. Each of these iterations should manifest a similar amount of electron energy reduction due to spin bonding, given the geometric similarity.
We might therefore expect the ‘per electron’ numbers for vanadium and manganese to be comparable, and they should also shed light on what chromium’s numbers might have been without the single-valence-electron issue. Manganese’s χm value is obviously larger than vanadium’s, though, because it has two more electrons (of roughly the same EME) contributing to its signature.
(See manganese (Mn) for more detail.)
(See below for the reason that manganese and the 3d metals before it are not ferromagnetic.)
*
Chromium (Cr):
Chromium is the only metal that is naturally antiferromagnetic at room temperature, though it loses this antiferromagnetism in favor of paramagnetism at a rather low Curie Temperature of 38ºC. Let us therefore first consider its paramagnetism. (See below for more on its antiferromagnetic state).
Chromium has the same electron configuration as manganese, with the exception that its 4s valence shell only contains a single electron. It is here proposed that this electron will have a disruptive effect on the unpaired electrons within, as it seeks the balance of a pair. This will consequently also disrupt any coherence between the atomic core electrons and an external magnetic field, which should have the effect of decreasing the effective magnetic signature of unpaired core electrons with respect to that magnetic field.
Chromium has a magnetic susceptibility value of χm=+167, which would represent an EME≈0.57e–. That equates to about only 0.11e– of electron signature contributed per electron. If the above conjecture is correct, the disruptive presence of the single valence s-electron in the conduction band appears to reduces the atom’s EME by as much as two thirds.
(See chromium (Cr) for more detail.)
SUMMARY:
4. Diamagnetism
Diamagnetism occurs when a substance is repelled from a magnetic field because it contains di-electrons. These paired electrons are in a state of perfect field cancellation with one another. The presence of an external magnetic field will disrupt the harmonic coherence of their di-electron states, raising energy. This causes the atom to repel away from the external magnetic field in search of a lower energy state.
Diamagnetic substances have negative magnetic susceptibility (χm) values.
ANALYSIS:
Zinc (Zn):
Zinc’s 3rd shell is full, with a symmetrical cubic arrangement of 8 field-repelling di-electrons, and its 4th shell has the 4s2 di-electron. This gives zinc a low magnetic susceptibility value of χm=–9.15.
*
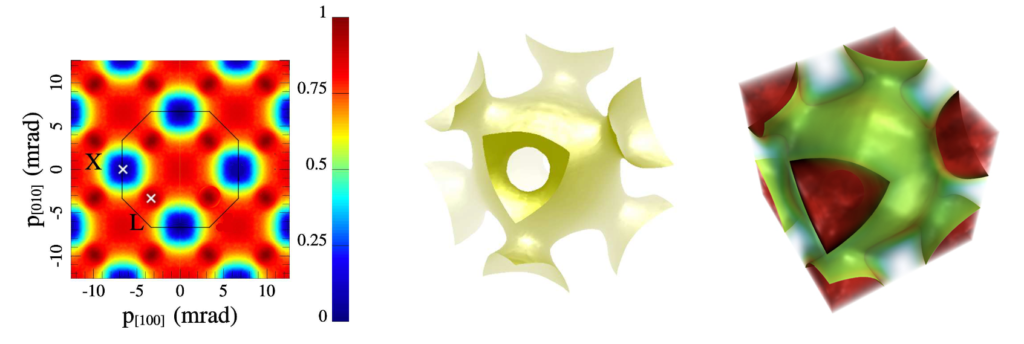
Copper (Cu):
Copper’s 3rd shell is full, with a symmetrical, cubic arrangement of 8 field-repelling di-electrons, just like zinc, however copper has a less diamagnetic value of χm=–5.46. It is proposed that, because it also has one unpaired 4s1 electron in its valence shell, that electron acts to disrupt the perfect diamagnetism of the di-electrons within it.
Observational evidence may bear out the proposed cubic structure of copper’s 3rd shell. The following images of copper’s Fermi surface were obtained by Weber (et.al.) using a process known as 2D-ACAR. [Ref]:
5. Ferromagnetism
Ferromagnetism occurs when the electrons in a substance are able to retain their internal crystalline magnetic field alignment after the external field that aligned them is removed. The solid can therefore act as a permanent magnet. This property therefore depends directly upon how well the unpaired electrons on adjacent atoms can link their spins and magnetic fields, thereby holding one another in alignment.
It is proposed [ref] that there are two criteria that are required in order for the atoms of a metal crystal to achieve ferromagnetic spin bonding, and thus, a crystal-wide ferromagnetic spin resonance.
- CRYSTAL GEOMETRY: For optimal spin bonding, unpaired core electrons should have an electron domain geometry that matches the crystal unit cell geometry. We propose that the 8-directional symmetries that arise as a result of pd-hybridization may provide these.
- SUFFICIENT ORBITAL EXTENSION: Unpaired core electrons require constriction and radial extension in order to interact (via spin bonding) with similarly extended core electrons on adjacent atomic cores in a crystal. We propose that this is achieved as a result of sufficient di-electron (electron pair) repulsion within the atomic shell, along with added repulsion from the di-electrons in the 2nd shell that lie directly beneath the unpaired core electron orbitals. This criterion is therefore intimately related to the electron geometry (from criterion #1 above), as well as to the number of same-shell di-electrons constricting the unpaired electron orbitals.
Only with both of these criteria fulfilled, will a transition metal be ferromagnetic. If only one is present, or if constriction and extension are not sufficient, the element will be paramagnetic.
6. Ferromagnetic Strength Trend
The following diagram shows the relative ferromagnetic strengths of the 3 ferromagnetic transition metals, along with the orbital geometries and orbital extension proposed for their unpaired electron orbitals.
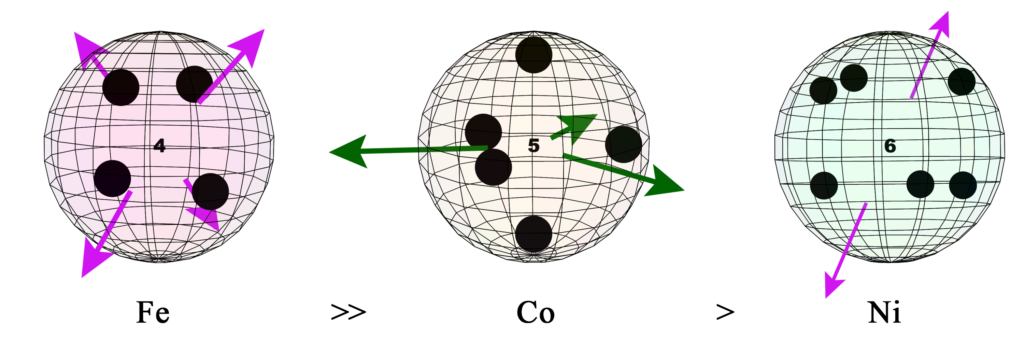
ANALYSIS:
Iron (Fe):
It is proposed that, in its ferromagnetic form, iron’s 3rd shell contains 4 di-electron orbitals and 4 unpaired electron orbitals in p3d5-hybridization, stabilized by the ‘fundamental’ of the 3s2 di-electron.
CRYSTAL GEOMETRY: Body-centered cubic (BCC) — when ferromagnetic
Iron has 4 unpaired electron orbitals in tetrahedral symmetry around the atomic cores. This is compatible with the (double tetrahedral) structure of a BCC crystal.
SUFFICIENT ORBITAL EXTENSION: by 8 di-electrons
Unpaired electron orbitals are constricted by 4 same-shell di-electrons, as well as by 4 di-electrons in the 2nd shell directly beneath them.
According to this model, iron has four instances of ferromagnetic spin bonding per atom. Not only is the geometry perfectly symmetrical, crystal-wide, but the unpaired electron orbital constriction and extension are also significant, caused by 8 di-electrons. It therefore makes sense that, compared to cobalt and nickel, iron would be significantly more ferromagnetic, which it is.
For more detail, see Iron (Fe)
*
Cobalt (Co):
It is proposed that, in its ferromagnetic form, cobalt’s 3rd shell contains 5 di-electron orbitals and 3 unpaired electron orbitals in p3d5-hybridization, stabilized by the ‘fundamental’ of the 3s2 di-electron.
CRYSTAL GEOMETRY: Hexagonal close-packing (HCP) and face-centered cubic (FCC) — when ferromagnetic
Cobalt has 3 unpaired electron orbitals in trigonal planar symmetry around the atomic cores. This is compatible with the structures of both HCP and FCC crystals. In its ferromagnetic state, cobalt assumes an HCP crystal structure below 450ºC, and an FCC structure above it.
SUFFICIENT ORBITAL EXTENSION: by 7 di-electrons
Unpaired electron orbitals are constricted by 5 same-shell di-electrons, as well as by 2 of the 4 di-electrons in the 2nd shell beneath.
According to this model, cobalt has three instances of ferromagnetic spin bonding per atom. Not only is the atomic geometry within the crystal primarily symmetrical in two dimensions — trigonal planar within the hexagonal layers — but the unpaired electron orbital constriction and extension are only caused by 7 di-electrons. It therefore makes sense that, compared to iron, cobalt would be significantly less ferromagnetic, which it is.
For more detail, see Cobalt (Co)
*
Nickel (Ni):
It is proposed that, in its ferromagnetic form, nickel’s 3rd shell contains 6 di-electron orbitals and 2 unpaired electron orbitals in p3d5-hybridization, stabilized by the ‘fundamental’ of the 3s2 di-electron.
CRYSTAL GEOMETRY: Face-centered cubic (FCC) — when ferromagnetic
Nickel has 2 unpaired electron orbitals in linear symmetry around the atomic cores. This is compatible with the structure of a FCC crystal (given the crystal-wide linearity of the FCC unit cell diagonal).
SUFFICIENT ORBITAL EXTENSION: by 7 di-electrons
Unpaired electron orbitals are constricted by 6 same-shell di-electrons, as well as by 1 of the 4 di-electrons in the 2nd shell beneath.
According to this model, nickel has only two instances of ferromagnetic spin bonding per atom. Even though the atomic geometry within the crystal is face-centered cubic, the spin bonding connections are linear — in a sense, symmetrical in only one dimension. The unpaired electron orbital constriction and extension are also only caused by 7 di-electrons. It therefore makes sense that, compared to iron and cobalt, nickel would be less ferromagnetic than both, which it is.
For more detail, see Nickel (Ni)
7. Curie Temperature Trend
Iron is by far the most strongly ferromagnetic of the three metals, yet cobalt has a higher Curie Temperature. This means that, even though iron is more strongly magnetic, cobalt (Co) can hang on to its magnetization to a much higher temperature. That must mean its ferromagnetic spin resonance is stronger than iron’s. How might we explain this?
According to the present proposed model, we might speculate that the reason for this is as follows. Cobalt contains three instances of ferromagnetic spin bonding (FSB) per atom, and the resonance is essentially two-dimensional, in the hexagonal crystal layers. Iron contains four instances of FSB per atom, and the resonance is three-dimensional and perfectly tetrahedral throughout the lattice. This causes iron to have a far more significant ferromagnetic spin resonance throughout its crystal, making it more strongly ferromagnetic than cobalt.
However, each of cobalt’s three instance of FSB involves 3 electrons holding each other in spin resonance. Each of iron’s four instances involve only 2-electron resonances. As such, cobalt’s spin bonding resonances are stronger and will therefore be able to withstand higher temperatures without thermalization disrupting them out of resonance. It is therefore proposed that this is what gives cobalt a higher Curie Temperature than iron, in spite of its weaker ferromagnetic strength.
8. Why Only Fe, Co & Ni?
Of the 3d transition metals, only iron, cobalt and nickel exhibit ferromagnetism. The others are all paramagnetic, except for copper and zinc, which are diamagnetic, and chromium, which is antiferromagnetic (at room temperature).
It is proposed that the transition metals of the 3d block that precede iron — scandium through manganese — are paramagnetic and not ferromagnetic because they do not have sufficient orbital constriction and extension of their unpaired electron orbitals. This would appear to be because the unpaired electron orbitals are sharing the shell with only 3 di-electrons.
It is unclear as to why criterion #2 appears to have a threshold of 4 di-electrons (in the case of the 3d transition metals), though we might speculate that it is because then at least half of the hybrid shell contains di-electron density, along with a consequently large amount of orbital constriction. (This would only be true from iron onward.)
WHY IS MANGANESE PARAMAGNETIC?
Why is manganese (Mn) paramagnetic (see above) and not ferromagnetic? It has the same electron geometry as cobalt, which is ferromagnetic, and manganese even has two more unpaired electrons than cobalt.
According to the present model, criterion #2 of ferromagnetism is not fulfilled. It is proposed that, with only 3 di-electrons constricting manganese’s 3rd shell unpaired electrons, its unpaired electron orbitals do not experience sufficient orbital extension to activate ferromagnetic spin bonding.
(See below regarding the antiferromagnetism of chromium (Cr).
9. Antiferromagnetism
Antiferromagnetism is a state in which the unpaired electron spins on adjacent atoms in the metallic crystal are anti-parallel to one another. This creates a net spin-zero state for the crystal as a whole, and it will therefore not exert an external magnetic force. As will be clarified below, it is proposed that antiferromagnetism is not a form of ferromagnetism, but rather a ‘local’ resonance resulting from an electron-gas coupling.
Chromium (Cr):
As mentioned above, chromium is the only metal that is naturally antiferromagnetic at room temperature, though it loses this antiferromagnetism in favor of paramagnetism at a rather low Curie Temperature of 38ºC.
This means that there is something about chromium’s electron structure that, when it is in crystalline metallic form at room temperature, its lowest energy state occurs when the electrons on adjacent atoms in the crystal are oriented with a magnetically antiparallel arrangement within its body-centered cubic (BCC) structure.
(NOTE: In the case of electrons, magnetically antiparallel does not mean the same as opposite spins. The former is a magnetic alignment distinction; the latter is a spin component phase relationship. Electrons of opposite spin can be either magnetically parallel or antiparallel. In the case of Hund’s 2nd Rule, adjacent degenerate electrons will both align magnetically parallel and will have the same spins, in order to create the lowest energy composite state. [ref])
The precise mechanism behind chromium’s antiferromagnetic state remains a matter under investigation, though it is believed to relate to the Fermi surface geometry within the crystal (rather than the crystal periodicity itself). [Ashcroft, Ch. 33].
If we were to speculate, based upon the present sub-quantum mechanical model, it seems plausible that the driving force behind causing the electrons on adjacent atoms to align their magnetic moments antiparallel and their spins opposite might be the pairing up of the 4s1 electrons, from adjacent atoms, in the electron gas. This might then cause the degenerate, unpaired pd-hybrid electrons to orient their spins to match the spin of their valence electron, in order to resonate mutually at the lowest energy. (Their coherence might explain why and how they both determine the Fermi surface in a crystal.)
If this conjecture is correct, it would account for why none of the other 3d transition metals are naturally antiferromagnetic. Each of the other 3d metal atoms contributes 2 valence electrons to the electron gas. They therefore do not require a valence electron of opposite spin from an adjacent atom in order to find the stability of an electron coupling (or, at least, a spin-zero average), and this form of coupling is therefore not present to anti-align the core unpaired electron orbitals of adjacent atoms. (Copper is an exception, since it also donates a valence electron into its core… although it contains no unpaired core electrons, which is why it is diamagnetic.)
According to this conjecture, it would seem that chromium’s antiferromagnetism does not arise from a crystal-wide spin-bonding resonance, as it does in the case of ferromagnetism. (It would therefore not be a form of ferromagnetism. It is proposed that chromium’s unpaired electron orbitals do not experience sufficient orbital extension to be ferromagnetic, due to constriction from only 3 same-shell di-electrons.) Consequently, the crystal structure of chromium — which is body-centered cubic (BCC) — should have no meaningful bearing on the mechanism behind its antiferromagnetism (as it would have in the case of a ferromagnetic crystal).
It is therefore proposed that the antiferromagnetism of chromium arises from an electron coupling resonance within the (valence) electron gas that binds the crystal. (This region is where the above-mentioned Fermi surface, as well as the valence and conduction bands are located.) Thus, even though the unpaired core electrons are not significantly extended, it is proposed that they do not need to be in order to resonate in degeneracy — to couple — with their own valence electron. (Perhaps we might even think of it as a kind of ‘local paramagnetism.’)
Since the coupling valence electron from each adjacent nearest-neighbor atom will have opposite spin, the (magnetic) core electrons of these adjacent atoms will therefore have opposite spins.
When the temperature increases enough to reach the Curie temperature, however, there is enough thermalization present to disrupt this weak electron gas coupling resonance, to the point where an external magnetic field will overwhelm it in favor of a crystal-wide paramagnetic alignment with the now-dominant external field. If this field is removed, the crystal will remain paramagnetic — with random magnetic alignments of the core electrons — until it cools below its Curie Temperature, at which time the electron gas coupling resonance can gain enough ‘traction’ over thermalization to re-enable antiferromagnetism.
10. Other Forms Of Magnetism
There are also other forms of magnetism, for example ferrimagnetism, altermagnetism, and an effect known as ‘spin glass‘ involving neodymium (Nd), but these will not be investigated here
References:
See DeMystifySci Podcast: The Strange Behavior Of Humans And Magnets for a brief video discussion of this concept.
J.G. Williamson, M.B. van der Mark, ‘Is The Electron A Photon With Toroidal Topology?’, Annales de la Fondation Louis de Broglie(1997) J.G. Williamson, A. Benn, M. Rudolph, ‘Quantum Spin Coherence In 4 Derived 3-Spaces’, Quicycle Journal (2022) A. Benn, J.G. Williamson, ‘pd-Hybridization And The Electron Geometry Of Fluorine, Neon And Iron’, Quicycle Journal (2024)
BACK TO PERIODIC TABLE