Understanding Electrons

RETURN to Periodic Table

The Nature Of Electrons

Electrons were discovered by J.J. Thomson in 1897. Their properties (like charge and mass) could be measured, but nobody knew what caused them. Electrons were therefore believed by many to be point particles with no substructure, to which their properties were simply attached.

Electrons are also believed by many to be much smaller than a proton, being almost 2,000 times lighter. However, in the hydrogen atom, for example, the electron is the size of the atom. Experiments in solid state physics have also shown that electrons can actually be many times larger than an atom (see Misconception Series: The Size of the Electron).

A century after J.J. Thomson’s discovery, in 1997, Dr. John G. Williamson and Dr. Martin B. van der Mark proposed a specific substructure for the electron.[1,2] For the first time, there was a rigorous model — accompanied by a powerful and fully relativistic mathematics [3] — that allowed us to probe inside the electron.

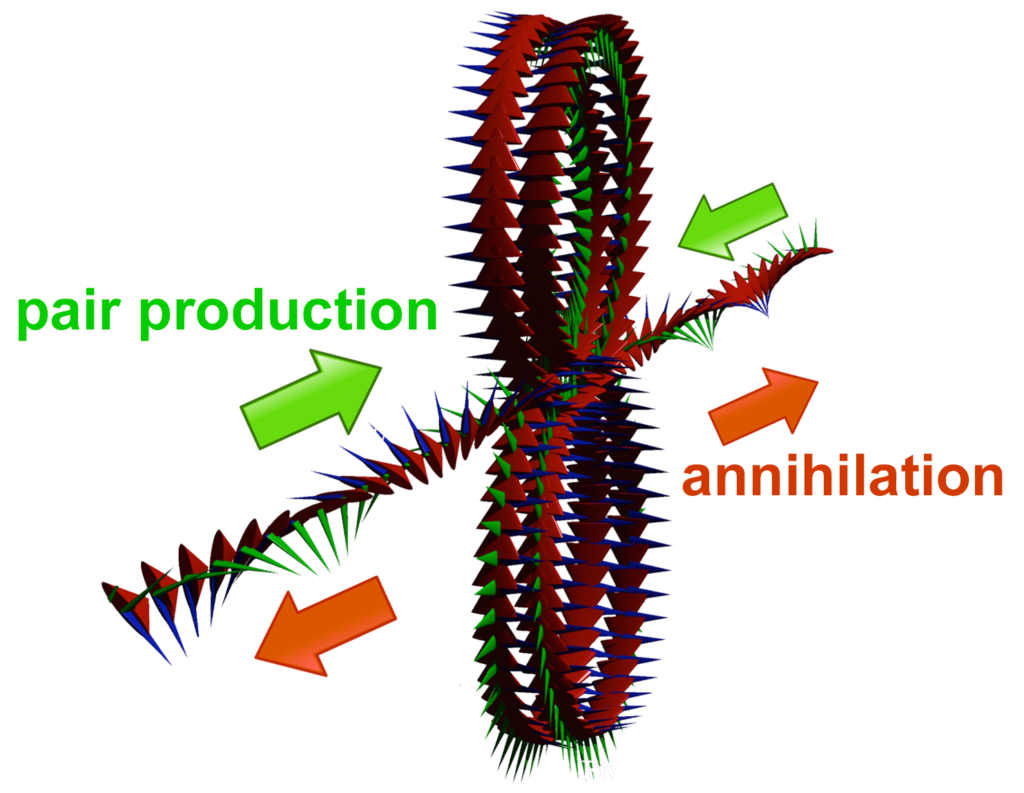
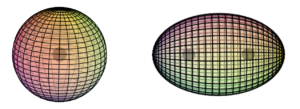
Each particle contains a confined photon making two complete revolutions for every one wavelength, resulting in a phase-locked, stationary wave of toroidal topology that defines the particle.

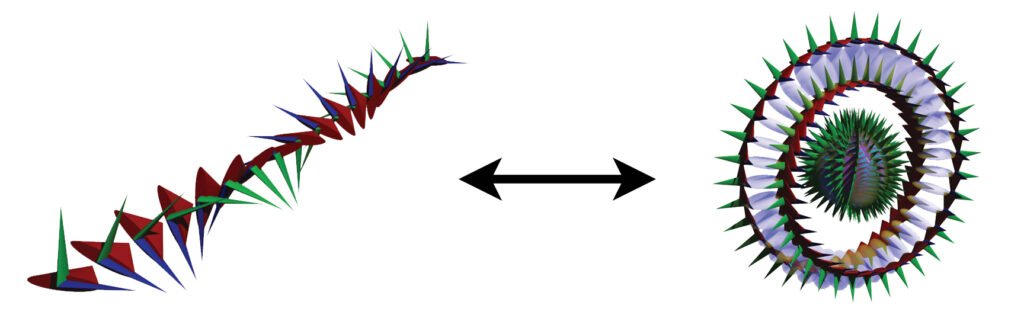
The snapshot of the electron (above, right) can be misleading because it is really many images combined. In normal space, each lens-shaped disk represents a slice through the same spherical distribution. The toroidal (donut) shape represents the phase-locked path of the rotating photon in momentum space (spatial frequency space ). In order to conserve the circularly-polarized photon’s angular momentum, the toroid will also tumble in space like a head-over-heels spinning ring (). The sphere in the center represents the result of this — a projection onto normal 3-dimensional space of the electron’s charge distribution, which is perfectly spherical in normal “space-space” ().

An isolated electron is thus a self-confined knot of concentrated energy traveling around itself at the speed of light. ( CLICK HERE to see one of John Williamson’s lectures on the electron’s structure.)

As a result of this model, we can now make far more significant conjectures about the source of its properties, like charge and mass, and even of quantization itself. More significantly, this proposed topology allows the elementary charge — the charge of the electron — to be calculated.

This is a noteworthy accomplishment! No prior theory of the electron has been able to accomplish this. (Click HERE for more details about this calculation.)

This revolutionary new “Sub-Quantum Mechanics” explains (and unifies) the electron’s shared particle and wave nature, and it similarly — and notably — bridges the gap between the quantum and classical realms. While an electron is a particle, its underlying nature is electromagnetic, containing a photon, which itself has both wave and particle properties. It is held together by a powerful coherence, far stronger than the strong nuclear force, here dubbed the “super strong force.” Furthermore, it is these topologies — hbar of photon angular momentum and ½hbar of internal particle angular momentum — which lie at the very heart of quantization itself.

Electrons are harmonic stationary waves that have electric charge, magnetic field, and angular momentum, and they are affected by the charge, field, and spin of other particles in their vicinity. As a result, when multiple electrons interact in the same atom or molecule, they produce orbital regions that are symmetrical, phase-locked, resonant, coherent, spherically-harmonic, stationary electron waves. These stationary waves represent a maximum symmetry state of the system, incorporating regions of positive and negative wave interference. Note that within this new theory of quantum electromagnetism, these coherent states need not be simply the lowest energy states. Quasi-stable coherent states of higher energy may include, for example, a spin coherence (see below).

The entire atomic system forms a single, coherent, harmonic quantum state. Each electron within this state can no longer be seen as an independent particle but is an essential component of the harmonic electron stationary wave. Any addition or subtraction of energy or electrons will cause the entire system to snap into its next most stable harmonic state.

The image above is made with a rotating string, and it evokes the idea of a resonant stationary wave in the linear direction.

The images below represent 3 different views of the 4 degenerate hybrid orbitals of the carbon atom’s second shell — the 4 equivalent tetrahedral sp³ orbitals. The center and right images (below) are intended to evoke a more realistic idea of this spherically harmonic resonance wave in 4 directions. It results in 4 equivalent ‘antinodes,’ which maintain complete filling of the spherical second shell of the atom in order to cancel electric field with the nucleus in every direction. Nodal boundaries of low (though non-zero) electron density in electric field space might separate each orbital “slice” within the shell.

Within each orbital slice, electron density will almost certainly be highest at the center of the face of each orbital, and will decrease toward the nodal regions that ‘divide’ the orbitals, where electron density will be lowest (though not zero).

Electrons In Atoms

NUCLEAR ATTRACTION
Electrons are present because they are attracted into the positive charge well of the nuclear protons. As electrons arrive, they will try to approach and envelop the nucleus with a simple spherical symmetry. In the hydrogen (H) atom, its single electron creates a spherical s-orbital. The helium (He) nucleus attracts two electrons, which merge into the di-electron state (see below) and are thus both able to surround the nucleus in the same (superimposed) s-orbital symmetry. If there is already a spherical di-electron shell, new electrons will be impeded from approaching the nucleus. They will therefore cluster around the core electrons in a symmetrical fashion, forming a second shell around the first — a single-electron second shell in the case of lithium (Li), and a second concentric di-electron shell in the case of beryllium (Be). Note carefully, however, that these shells are not really separate at all. They are structural elements within a single harmonic wave coherence — a single atom-sized quantum system.

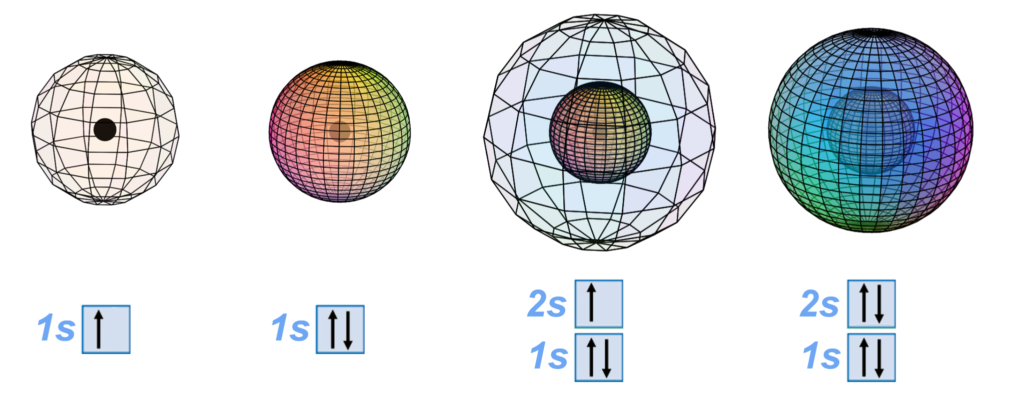
Perfect spherical symmetry is lost with the 5^th element, boron’s, 5^th electron. From that point on, atoms must subdivide their electron shells in order to achieve symmetrical, harmonic, and stable stationary wave structures around a spherical core. When additional electrons compete with the second-shell di-electron for the privilege of approaching the nucleus, the volume of the outer shell becomes subdivided in a symmetrical fashion, and electrons find their positions in the resulting orbital resonance by submitting to the relative strengths of their interactions. (See Hybridization below.) Electron orbital geometry is therefore a function of distance from the nucleus, as well as charge (vector), field (bi-vector), and spin (tri-vector) interactions.

TOTAL Di-ELECTRON INCLUSION (TDI):
How is it possible for electrons in an atom to pair up when they have the same charge, since like charges repel? In fact, they pair up so forcefully that their pairing forms the covalent bonds that hold atoms together in molecules and that give the diamond crystal its hardness.

When two electrons of opposite spin envelop a nucleus, they will snap into an antiparallel magnetic alignment because this allows them to superimpose completely upon one another. Their magnetic fields are then oppositely aligned at every point, resulting in maximum magnetic field cancellation, which lower energy significantly. All three components of the electrons’ quantum spins are now also oriented in such a way that they are able to flow through one another, counter-rotating and ‘interweaving’ to form a powerful spin coherence. This locks the electrons together through angular momentum linkage, and lowers energy further by lowering overall angular momentum. (For more on the nature and components of the electron’s spin, see our Quicycle Journal article “The Photonic Topology Of Quantum Spin” or the video The Physics Of Sub-Quantum Spin.)

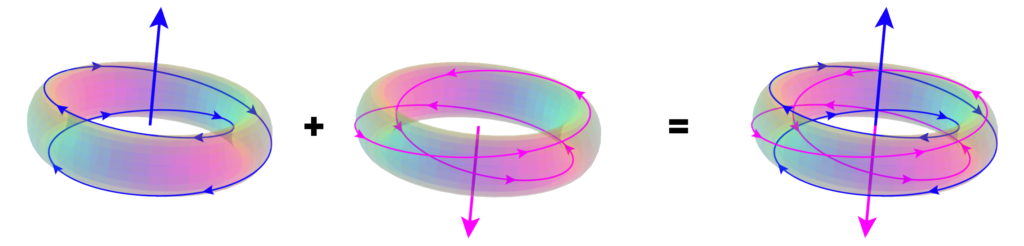
These interactions, collectively named Total Di-Electron Inclusion (TDI), give rise to the di-electron state that is, for example, the helium (He) atom’s 1s² shell. This di-electron is a boson state, which is a distinct state from that of two individual electrons (which are fermions).

When two electrons on adjacent atoms have opposite spins, they can be attracted into this superimposed di-electron state, giving rise to a single covalent bond, as in the hydrogen molecule (H₂). The lowering of energy from magnetic field cancellation and spin coherence is the attractive force that holds the atoms together. The two proton nuclei remain suspended within the di-electron by the attraction of opposite-charge electric field cancellation, but they remain a distance apart from one another due to the field intensification of like-charge proton repulsion. A molecule can thus be thought of as a discrete crystal-like unit — positive cores suspended in a 3-dimensional “electron gas.”

THE PAULI EXCLUSION PRINCIPLE & HUND’S 2nd RULE:
If the spherical s-orbitals are full, new electrons must resonate as non-spherical p-orbitals (or higher). This no longer allows the electron density to achieve spherical symmetry around the spherical atomic core. Since the electrons can no longer superimpose as a result of geometric constraints, asymmetry raises resonance energy and decreases coherence. Electrons therefore seek symmetry by venturing into the next (and slightly) higher energy harmonic coherence state — that of parallel spin.

Since they are no longer at immediately close range, electrostatic repulsion has primacy and magnetic and spin effects become less influential. This is because the (dipole) magnetic force drops off as the inverse cube (1/r³) of distance whereas the (monopole) electric charge drops off as the inverse square (1/r²) of distance. Since the electric force drops off more slowly than the magnetic force, it is stronger at distance.

This explains the physics behind the Pauli Exclusion Principle. This is electric and magnetic field exclusion in order to avoid the energy increase associated with constructive field interference. The sum of these interactions causes the electrons to move as far from each other as their atomic geometry will allow.

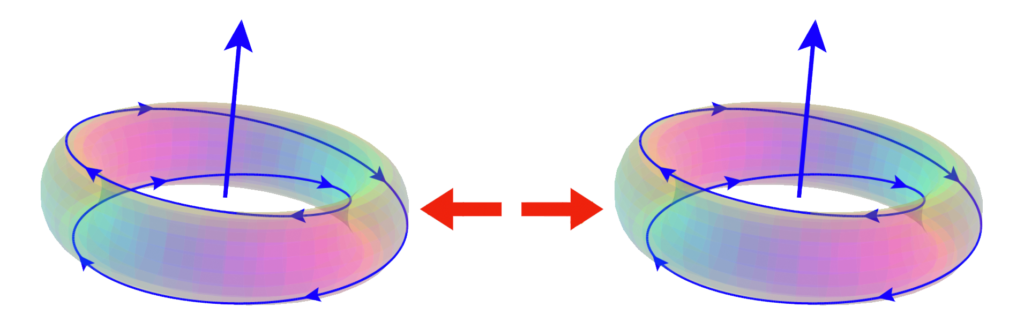
At that point, the forces of charge repulsion and atomic geometry achieve balance, and the weaker spin interactions can therefore emerge (in the hierarchy of forces). This is where the ‘intrinsic’ and ‘toroidal’ components of quantum spin come into play. (see The Physics Of Sub-Quantum Spin for more detail.)

Adjacent electrons will experience spin phase interactions differently to superimposed electrons. What may have been an energy increasing spin interaction when superimposed, may have become an energy decreasing spin interaction.

The diagrams below illustrate the ‘harmony of phase’ energy interactions between the proposed components of the electron’s ‘sub-quantum’ spin, demonstrating why adjacent, magnetically parallel, and same-spin electrons result in the lowest energy resonance. They experience both toroidal and intrinsic spin counter-rotations, ‘spin interweaving.’ This would lower energy, creating a more favorable quantum state.

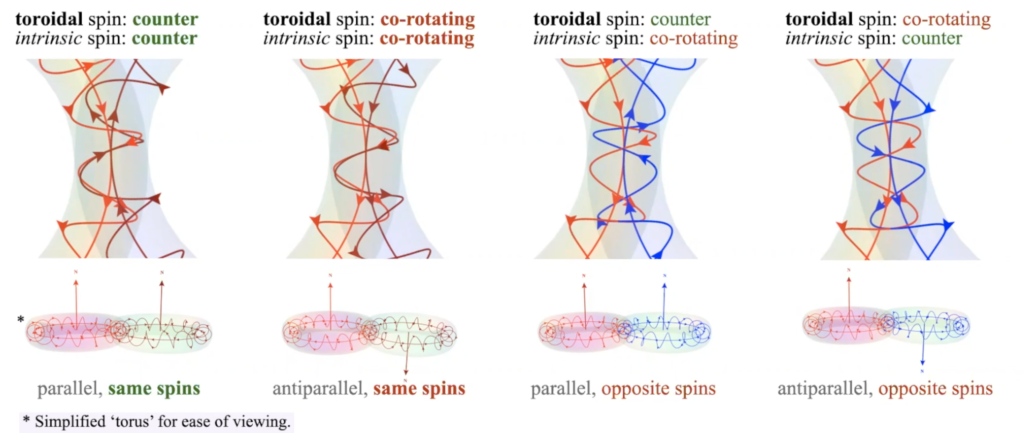
It is proposed that these spin interactions explains the physics behind Hund’s 2^nd Rule, that adjacent, same-shell electrons will have lowest overall energy when they possess like spins. If they posses opposite spins, when they are adjacent, their intrinsic spins will interact in a way that increases energy.

PARALLEL SPIN BONDING (PSB):
This process is here dubbed “Parallel Spin Bonding.” Once electrons with parallel alignment and same spins achieve the maximum allowed distance from one another, the forces of charge repulsion are in balance and, it is proposed, the electrons are thus able to link their lowest energy spin interactions into a single, larger, coherent, multi-electron quantum spin coherence. This lowers energy and pseudo-stabilizes these otherwise unpaired equal-energy (degenerate) electrons.

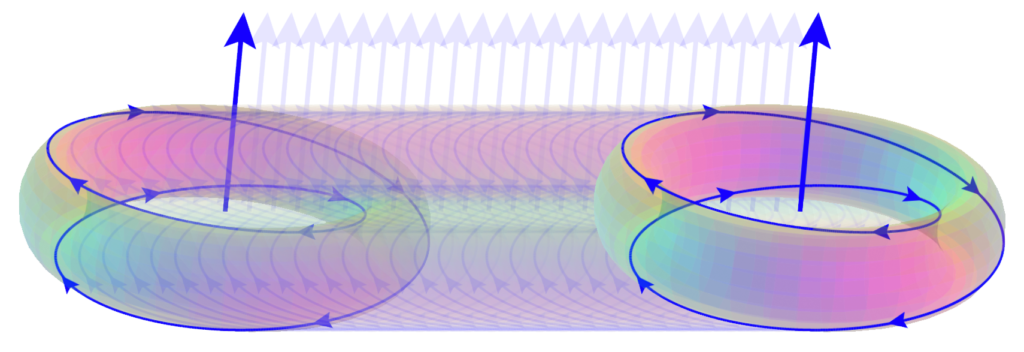
Degenerate electrons that are unable to superimpose will therefore preferentially assume parallel, same-spin states, creating a more favorable energy condition, with spin bonding, out of one that is otherwise less stable than the preferred di-electron state.

This is what occurs during hybridization. In the sp² hybridization of boron (B), which we will discuss further below, the 2s² electrons uncouple from their di-electron state and elevate their energies, so that the single p-electron can lower its energy. The three electrons can then find symmetry and coherence as a set of trigonal planar, degenerate, spin-bonding electrons — a tri-electron state. Spin bonding compensates for the energy increase of electrostatic repulsion by lowering energy through the stabilization of quantum angular momentum linkage.

The Pauli Exclusion Principle thus embodies the process of charge and field exclusion, and Hund’s Rule embodies the energy decrease associated with Parallel Spin Bonding (PSB) in order to create the next most favorable electron energy state after the di-electron state. (see The Physics Of Sub-Quantum Spin for more detail.)

ELECTRON-Di-ELECTRON REPULSION:
When both unpaired electrons and di-electrons are present in the same shell, di-electrons will repel more strongly than unpaired electrons. This occurs due to the significant lowering of energy from field cancellation that takes place during di-electron formation, but this energy is raised if another field is allowed to interact (and interfere) with it. This is the reason diamagnetic substances repel magnetic fields, and di-electrons will similarly repel the fields of nearby unpaired electrons more strongly than unpaired electrons will repel one another.

As a consequence, electron orbital geometry will be dominated by di-electron geometry, and unpaired electrons will be repelled into secondary (symmetrical) positions as a result.

Orbitals & Orbital Hybridization

ELECTRON ORBITALS:
When multiple electrons interact in the same atom or molecule, they produce orbital regions that are symmetrical, phase-locked, resonant, coherent, spherically-harmonic, stationary electron waves. Each section or ‘tuft’ within a shell is a region of orbital electron density within this resonance that is typically occupied either by a single electron or a di-electron. The resulting geometry is therefore a consequence of nuclear attraction, mutual electron and di-electron repulsion, and quantum electron interactions. When an electron shell contains multiple orbital sections, the like-charge repulsion between them causes them to separate as much as possible in order to minimize repulsion. This requires spherical symmetry, and Platonic geometry provides us with a foundation on which to consider it. Orbitals will stray from perfect Platonic symmetry, however, when they contain either an odd number of electron domain directions or a combination of unpaired electrons and di-electrons, since di-electrons contain more electron density and repel more strongly than single electrons.

The wave structures that are the orbitals are separated by nodes of low (though non-zero) electron density, as seen in the orbital resonance of carbon shown above (and above, 2^nd from left). Each orbital can therefore be thought of as forming a part of a continuous spherical resonance structure — a phase-locked spherical stationary wave — that surrounds the nucleus in the most symmetrical, stable energy state it can achieve. (An analogy in the linear case might be a resonating string, shown above, where the symmetrical tufts (or bulges) in the wave appear to remain fixed in location and are separated by nodal points of low amplitude.)

Each electron and each di-electron occupies a discrete region within (and at the same time constitutes) this single coherent atomic (or molecular) resonance. This implies that electrons need not “orbit” the nucleus at all in order to remain connected to it. (Spin is an internal electron property. It does not arise from orbiting the nucleus.) On the other hand, a more accurate way to consider this state might be to focus on the energy flow within the coherent harmonic system, rather than considering the elements of it as discrete particles. It is, in fact, their lack of perfect discreteness that allows them harmonic coherence. 

Adding to or removing electrons (or photons) from this atomic resonance state causes it to snap into the next (either higher- or lower-energy) stable harmonic resonance state. The difference in energy between these harmonic resonance states represents the amount of energy arriving or leaving the atom during the transition.

ORBITAL HYBRIDIZATION:
Electrons strive to maximize symmetry and minimize repulsion. The way that orbitals achieve this is known as hybridization. It is when orbitals — that we normally designate as having different energies and geometries, like s– and p-orbitals — combine and rearrange themselves into a symmetrical arrangement of identical energy states. Overall, this symmetrical state has a lower energy than the sum of the individual energy states before they hybridized.

Hybridizations like sp, sp², sp³, sp³d, and sp³d² are familiar concepts. The first instance of it occurs in the boron atom with sp²-hybridization. With five electrons, boron is the first atom to contain electrons that are in a p-orbital. This is not a sphere-shaped harmonic, and so a single electron in a p-orbital cannot find a symmetrical arrangement around a sphere by itself. Boron therefore cannot simply add its p-electron on top of the same (2s²) configuration that beryllium has, as shown below, because it would not be stable:

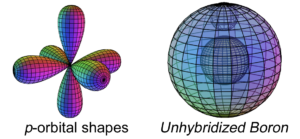
The asymmetry therefore causes the two electrons in the 2s orbital to uncouple from their di-electron state and form a tri-electron state with the single p-electron. Three equal-energy (degenerate) electrons can now achieve maximum stability by assuming a trigonal planar (sp²-hybridized) arrangement around the core electron shell, because this minimizes their mutual repulsion by having them as far from one another as they can get. (The wireframe indicates the boundary of the n=2 shell.)

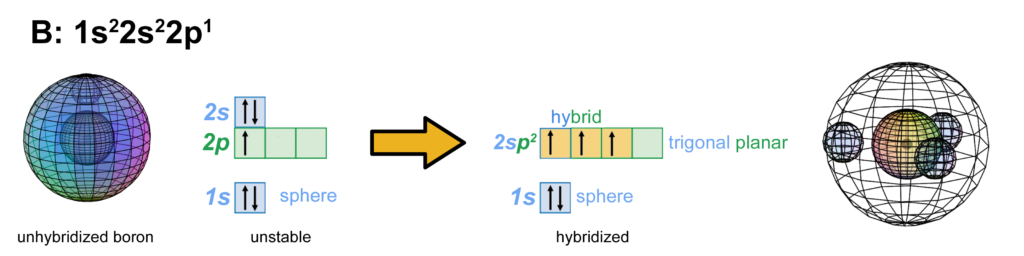
The outer spheres in the image above (on the right) simply indicate the directions of maximum electron density. The orbitals themselves will be more like three equal longitudinal sections. Each orbital occupies one third of the volume of the shell, though not uniformly, as electron density has a maximum at the center of the orbital and decreases towards the orbital boundary. But electron density will nonetheless fill the entire shell in order to shield the positive charge of the nucleus. In the case of boron, each of the three hybrid orbitals contains one electron.

In the case of carbon (C), the sp³-hybridization that occurs allows the atom to achieve tetrahedral symmetry involving the s-orbital and three p-orbitals of the 2^nd shell. Carbon’s electron configuration is 1s²2s²2s². Like boron, carbon cannot simply add its two p-electron into the same (2s²) configuration that beryllium (Be) has, as shown below, because it would not be stable:

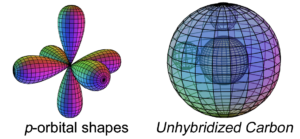
The asymmetry therefore causes the two paired electrons in the 2s orbital to uncouple from their di-electron state in order to form a tetra-electron state with the two p-electrons. The four equal-energy (degenerate) electrons can now achieve maximum stability by assuming a 4-directional (tetrahedral, sp³-hybridised) arrangement around the core electron shell. This minimizes repulsion by having them as far from one another as they can get.

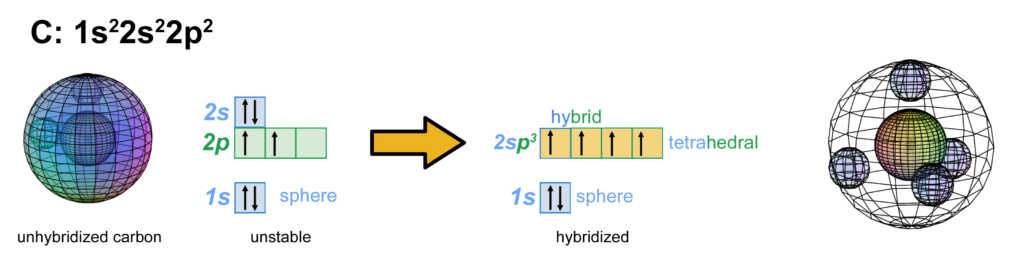
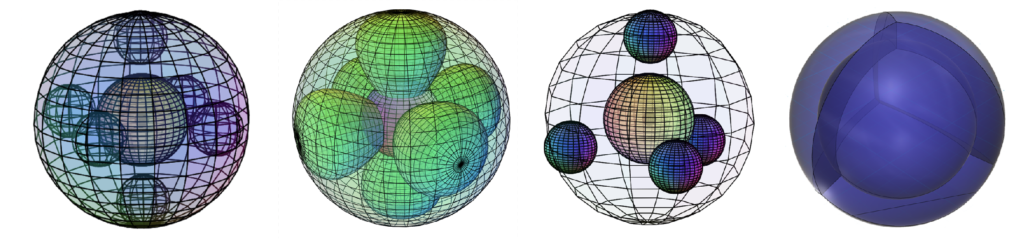
The small spheres within the 2^nd shell in the image above (right) simply indicate the directions of maximum electron density. The orbitals themselves will be more like four equal tetrahedral sections that can only occupy volume within their shell (see below). Each orbital occupies one fourth of the volume of the shell, though not uniformly, as electron density has a maximum at the center of the orbital and decreases towards the orbital boundary due to electron repulsion. But electron density will nonetheless fill the entire shell in order to shield the positive charge of the nucleus in every direction. In the carbon atom, each of the four hybrid orbitals contains one electron.

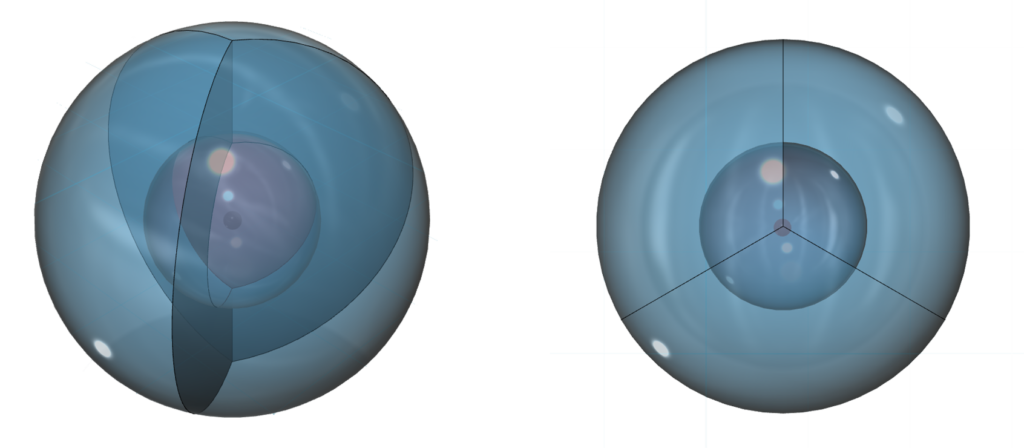
Four-directional (tetrahedral) symmetry is significant because, after the sphere, it is the first multi-directional symmetry that can attain perfect spherical symmetry. While the three-directional (sp²) symmetry of boron is symmetrical in the equatorial dimension, it is not spherically symmetrical since its axial electron density will be lower than its equatorial electron density.

In the case of neon (Ne), at the end of the second row of the periodic table, there is a full valence shell containing 8 electrons. The traditional view of the full 2^nd shell involves a spherical 2s² orbital di-electron, with 6 p-electrons resonating within it in mutually orthogonal directions (below, left). It is proposed, however, that the most symmetrical and lowest energy state for neon is achieved with 4 di-electrons in spherical tetrahedral symmetry (below, right). The 8 electrons sharing the small second valence shell would achieve lowest energy if they paired up, since field cancellation is maximized in di-electron formation. This also allows the distance between the regions of maximum electron density in the orbital lobes to be the greatest, which minimize repulsion more effectively.

If that is the case, the electron configuration of argon (Ar) should produce two nested spherical tetrahedra, aligned antiparallel, as shown below.

The reason that this nested antiparallel tetrahedral geometry is so stable is that the region of lowest electron density on one shell lines up with the region of highest electron density on the adjacent shell, thereby minimizing repulsion. In the diagram on the left above, the vertex where the nodes between orbitals intersect is a point of lowest electron density. It lies directly opposite the center of the face of the orbital above or beneath it, which is the point of highest electron density in that orbital. This overlap is therefore the lowest energy state.

Like oxygen, the sulfur (S) atom contains 6 valence electrons arranged into two di-electrons and two unpaired electrons. An example of sp³d²-hybridisation occurs when a sulfur atom is approached by a highly electronegative atom like oxygen or fluorine. Their high electronegativity can induce one or both of sulfur’s valence di-electrons to uncouple, yielding up to 6 unpaired electrons available for bonding. This is possible for sulfur but not for oxygen because the 3^rd shell contains a larger volume than the 2^nd shell, which is the reason it can accommodate a d-orbital. While sulfur does not usually have electrons in its 3d-orbital, the 3^rd shell has enough volume to accommodate the additional electron density. This allows sulfur’s electrons to hybridize into more electron domain directions than a 2^nd row element. Sulfur can therefore make up to 6 covalent bonds, as we see in the octahedral case of sulfur (shown below), as found in the sulfur hexafluoride (SF₆) molecule.

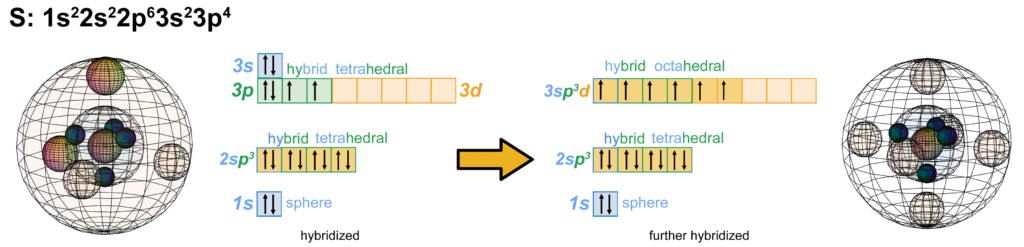
While this octahedral symmetry looks just like the structure of the p-orbital shown earlier, it is important to note that it is not made up of just p-orbitals. It is a hybrid that combines the 3s-, 3p-, and 3d-orbitals. In fact, if the structure proposed above for neon is correct, it would mean that there is no actual case in nature where p-orbitals exist in three mutually orthogonal directions, as they are modeled in the traditional way. When p-orbitals are present along with other orbitals in the same space, they must always hybridize because close-range electron interactions in the same atomic shell cannot be avoided.

In addition, this approach allows for the speculation of a new type of orbital hybridization that involves interactions between p-, d– and f-orbital electrons when they occupy the same shell. It is proposed that the resulting electron geometries help explain the magnetic properties of the transition and rare earth metals. (See pd-hybridization)

RETURN to the Periodic Table